Area Of A Triangle And Its Circumradius

We read about circumradius and circumcentre . Today we are going to see a useful relation between the circumradius and the area of any triangle.

$\underline{Theory}$

If the area of a $\triangle ABC$ is denoted by $\Delta$ and its circumradius is denoted by $R$, then

$4\Delta R = abc$ where $a,\ b,\ c$ are the three sides of the triangle.

$\underline{Construction}$

Let $\triangle ABC$ be a triangle with circumradius $O$. Let us draw the altitude $AP$ from the vertex $A$ to $BC$. We join points $A$ and $O$ and extend $AO$ to meet the circumcircle at $D$, making $AD$ the diameter of the circle. Let us join $BD$.

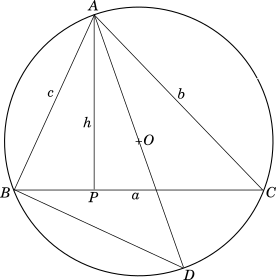
-----------book page break-----------

Let the lengths of the three sides be $a,\ b,\ c$ and that of the altitude be $h$ as marked in the figure above.

$\underline{Proof}$

From the basic formula of triangle area, we know:

$ar[\triangle ABC] = \Delta = \dfrac{1}{2}ah$ $...eqn\ (i)$

Considering $\triangle s\ ABD$ and $APC$,

$\angle ADB = \angle ACB$ (angles subtended by the same arc $AB$ at the circumference)

$\angle ABD = \angle APC$ (both are $90^\circ$)

Therefore, the third angles $BAD$ and $PAC$ are also equal.

$\therefore \triangle ABD \sim \triangle APC$

Therefore,

$\dfrac{AP}{AB} = \dfrac{AC}{AD}$

$AD$ is the diameter of the circumcircle, therefore, is equal to $2R$.

$\therefore \dfrac{h}{c} = \dfrac{b}{2R}$

$\Rightarrow h = \dfrac{bc}{2R}$

Substituting this value of $h$ in $eqn\ (i)$ we get:

$\Delta = \dfrac{1}{2}a \times \dfrac{bc}{2R}$

$\Rightarrow \Delta = \dfrac{abc}{4R}$

$\Rightarrow 4\Delta R = abc$