Trigonometric Functions And Periodicity

We have learnt about the unit circle . We have seen that all trigonometric functions are periodic in nature. Today we will take a deeper look at the periodic nature of trigonometric functions.

I. Understanding Periodicity Of Simple Trigonometric Functions

Let us take a look at the diagram below:

-----------book page break-----------

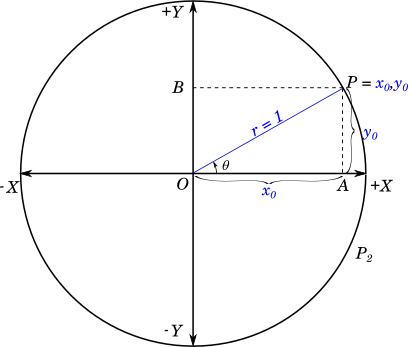
As the radius $OP$ point rotates in the positive direction (that is anti-clockwise) the values of the various trigonometric ratios change as we have seen in the previous booklet.

What happens when $OP$ completes one full rotation and coincides back with the positive $X$ axis?

Angle $\theta$ becomes $360^\circ$ (using radians notation we can write $360^\circ = 2\pi^c$ or simply $360^\circ = 2\pi$) or which is equivalent to $0^\circ$.

In our subsequent text we will use radian as a unit for angle, but whatever we discuss should be applicable for any unit the you may choose.

Let us say $OP$ continues to rotate and point $P$ reaches $x_0,\ y_0$ as shown in the previous diagram.

Now the value of the angle is $2\pi + \theta$, in radians. Since point $P$ is at $x_0,\ y_0$, all the trigonometric ratios will have the same values.

That is:

$sin\theta = y_0$

$cos\theta = x_0$

$tan\theta = \dfrac{y_0}{x_0}$

$cosec\theta = \dfrac{1}{y_0}$

$sec\theta = \dfrac{1}{x_0}$

$cot\theta = \dfrac{x_0}{y_0}$

Therefore using function notation we can say that $f(2\pi + \theta) = f(\theta)$, where $f$ is any one of the above trigonometric functions. This is true for all points $P$ on the circle.

-----------book page break-----------

Similarly, when $OP$ rotates by another $2\pi$ radians and comes back to point $P$, the values of all the ratios will repeat.

Therefore, we can say:

$f(4\pi + \theta) = f(2\pi + \theta) = f(\theta)$

Now we can see that we can keep on adding $2\pi$ to $\theta$ infinite number of times, but the values of $f(\theta)$ will remain unchanged.

So we can say the values of these trigonometric functions repeat after a fixed period $2\pi$

Let us take a look at the diagram below.

The blue line shows the plot of the function $sin\theta$ for $\theta$ ranging from $0$ to $6\pi$ radians.

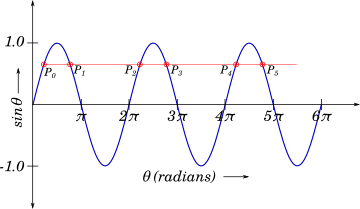
We can choose an arbitrary value of $\theta$, let's say $\theta = \dfrac{\pi}{3}$ radians $(60^\circ)$, the value of $sin\left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2} \approx 0.866$

-----------book page break-----------

Therefore the point $P_0$ on the graph is $\left(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2}\right)$. We draw a straight line passing through $P_0$ and parallel to the $X$ axis. Let us call the other intersection points of this line with the $sine$ function as $P_1$, $P_2$, $P_3$, $P_4$ and $P_5$.

The $y$ value ($sin\theta$) at each of these points is the same as the $y$ value of $P_0$, that is $\dfrac{\sqrt{3}}{2}$.

We know from our earlier topic of the unit circle, that $sin(\pi - \theta) = sin\theta$. Therefore, the $x$ value of $P_1$ is $\pi - \dfrac{\pi}{3} = \dfrac{2\pi}{3}$

Similarly the $x$ values of points $P_2,\ P_3,\ P_4$ and $P_5$ are $2\pi + \dfrac{\pi}{3}$, $2\pi + \dfrac{2\pi}{3}$, $4\pi + \dfrac{\pi}{3}$, and $4\pi + \dfrac{2\pi}{3}$.

Let us see when is the value $\dfrac{\sqrt{3}}{2}$ repeating.after the first value $\theta$ which is $\dfrac{\pi}{3}$.

The first repeat $(P_1)$ is after $\dfrac{2\pi}{3} - \dfrac{\pi}{3} = \dfrac{\pi}{3}$

The second repeat $(P_2)$ is after $2\pi$

The third repeat $P_3$ is after $2\pi + \dfrac{\pi}{3}$

The fourth repeat $P_4$ is after $4\pi$

The fifth repeat $P_5$ is after $4\pi + \dfrac{\pi}{3}$

Although we see that the first repeat $P_1$ is after $\dfrac{\pi}{3}$ we cannot take $\dfrac{\pi}{3}$ as the period. If it was the period then after another $\dfrac{\pi}{3}$ the value of $sin\theta$ should have been $\dfrac{\sqrt{3}}{2}$.

-----------book page break-----------

However the value of $sin\left(\dfrac{2\pi}{3} + \dfrac{\pi}{3}\right) = sin(\pi)$ is $0$ and not $\dfrac{\sqrt{3}}{2}$.

We can consider a value as the period if and only if, after $every$ period the value of the function is the same.

We can also see from the above plot that the value of the period can be $2\pi$ or $4\pi$ or $6\pi$ or any even multiple of $\pi$, because the value will repeat itself after every period, for all these values.

So are $4\pi$, $6\pi\ ,...$ periods for the $sine$ function? Indeed they are.

However, ordinarily when we talk about $periods$ we take the least value of the $period$, which is also known as the $fundamental\ period$.

Now we will see how period changes for functions where $\theta$ is multiplied by a coefficient.

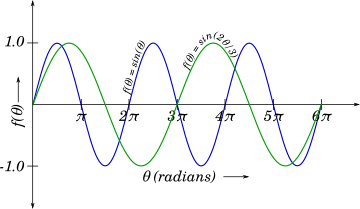
Let us plot the function $f(\theta) = sin\left(\dfrac{2\theta}{3}\right)$

The plot of this function is shown below in green, along with the previous function $f(\theta) = sin(\theta)$ shown in blue.

-----------book page break-----------

We can visually see that the plot of the function $sin\left(\dfrac{2\theta}{3}\right)$ completes on cycle when $\theta = 3\pi$

To understand this let us substitute $\dfrac{2\theta}{3} = \phi$.

So we get $f(\phi) = sin(\phi)$ which is our normal $sine$ function which completes one cycle when $\phi$ reaches $2\pi$

The value of $\theta$ when $\phi = 2\pi$, can be obtained by putting $\phi = 2\pi$ in the equation:

$\dfrac{2\theta}{3} = \phi$

$\Rightarrow \dfrac{2\theta}{3} = 2\pi$

$\Rightarrow \theta = 3\pi$

Similarly, for any function of the form $f\left(\dfrac{\theta}{\lambda}\right)$, where $f$ is any trigonometric function and $\lambda$ is a constant, the period will be $\lambda \times 2\pi = 2\lambda\pi$

II. Periodicity Of Sum Of Trigonometric Function

We can form a composite trigonometric function by adding or subtracting two or more simple functions.

For example, we can say that $f$ is a sum of two functions, if

$f(\theta) = f_1(\theta) + f_2(\theta)$

We can re-use the previously defined simple functions to form a sum.

Let:

$f(\theta) = sin(\theta) + sin\left(\dfrac{2\theta}{3}\right)$

The question is: what is the period of $f(\theta)$?

-----------book page break-----------

Earlier we saw that when we express a simple function as $f\left(\dfrac{\theta}{\lambda}\right)$, then the period is given by $2\lambda\pi$.

If the period of $f_1$ is $2\lambda_1\pi$ and the period of $f_2$ is $2\lambda_2\pi$, then the value of $f_1$ repeats after every interval of $2\lambda_1\pi$, and the value of $f_2$ repeats after every interval of $2\lambda_2\pi$.

Therefore, the earliest both of them will repeat together, is $lcm(\lambda_1,\ \lambda_2) \times 2\pi$, and that is going to be the period of the sum function.

We will write our sum function in the $\dfrac{\theta}{\lambda}$ form.

$f(\theta) = sin\left(\dfrac{\theta}{1}\right) + sin\left(\dfrac{\theta}{\frac{3}{2}}\right)$

Therefore, for our problem, $\lambda_1 = 1 = \dfrac{1}{1}$ and $\lambda_2 = \dfrac{3}{2}$

We know from , that the $lcm$ of two or more fractions is $\dfrac{lcm\ of\ numerators}{gcd\ of\ denominators}$

Therefore, $lcm\left(\dfrac{1}{1},\ \dfrac{3}{2}\right) = \dfrac{lcm(1,\ 3)}{gcd(1,\ 2)} = 3$

Therefore, the period of the resultant sum function is $3 \times 2\pi = 6\pi$

We can visually inspect the previous plot to see that $f_1$ completes $3$ cycles when $\theta$ reaches $6\pi$ and $f_2$ completes $2$ cycles when $\theta$ reaches $6\pi$, after which all values of $f$ will repeat.