Linear Equations

We learnt how to represent points on a Cartesian plane .

Today we are going to learn how to represent a straight line on a Cartesian plane.

$\underline{I.\ Representing\ Straight\ Lines\ On\ A\ Cartesian\ Plane}$

Let us start with a simple equation:

$y = 2x + 3$

The following points satisfy the equation:

$x = 0,\ y = 3$

$x = 1,\ y = 5$

$x = 2,\ y = 7$

$x = 4,\ y = 11$

$x = -1,\ y = 1$

$x = -2,\ y = -1$.

$x = 4.5,\ y = 12$

Like these points there are an infinite number of points that can satisfy this equation. This is not surprising since a line can have infinite number of points on it and each of these points can be represented on the Cartesian plane, using a distinct $X, Y$ values.

Now let us see how to plot a straight line on the Cartesian plane that will represent all these points.

We know that only a single straight line can pass through any two given points. Hence, to draw the line for the given equation we need to select any two of the above points and draw a line through those two points.

Let us select the points:

$x = 1,\ y = 5$ and $x = 4,\ y = 11$

-----------book page break-----------

Plot these two lines on the Cartesian plane and draw the line as shown below:

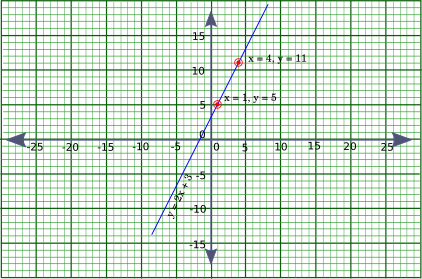
The line drawn in blue is the representation of the given equation: $y = 2x + 3$

As we can see, that all the points taken in the example lie on the line. You can verify that any other point lying on this line will satisfy the given equation.

Now let us look at a special type of equation with one variable missing.

Let's say we have the equation $x = 6$. As we can see that there is no $y$ in our equation.

The above equation can be interpreted as $\unicode{x201C}Whatever\ the\ value\ of\ y\ may\ be,\ the\ value\ of\ x\ is\ always\ 6.\unicode{x201D}$

To plot the line for the equation $x = 6$ we need to take two points on the Cartesian plane. Since $x$ is $6$ for all value of $y$ we can take any two values of $y$ of our choice and take the value of $x$ as $6$ for those two points.

-----------book page break-----------

For example we can choose $x = 6,\ y = 1$ as the first point, and $x = 6,\ y = 5$ as the second point.

Now, let us draw two points on the Cartesian plane, and draw a line passing through these points.

As you can see below, we have a line parallel to the $X$ axis.

Similarly we can draw the line $y = 9$ and obtain a line parallel to the $Y$ axis.

Both these equations are shown in the following diagram:

The line shown in purple represents the equation $x = 6$ and the line shown in blue represents the equation $y = 9$.

-----------book page break-----------

$\underline{II.\ Plotting\ A\ Line\ On\ The\ Cartesian\ Plane}$

Let us start by plotting a couple of simple equations on the Cartesian plane.

Let us start with the equation $x + y = 6$

We know that given two distinct points on any plane we can draw $one\ and\ only\ one$ straight line passing through both the points.

Therefore, if we can find two distinct set of $x,\ y$ values satisfying the given equation, then the line joining the two points will be our required line.

The easiest way to do this is to take $x = 0$ and find the corresponding value of $y$ and for one more point put the value of $y$ as $0$ and find the value of $x$.

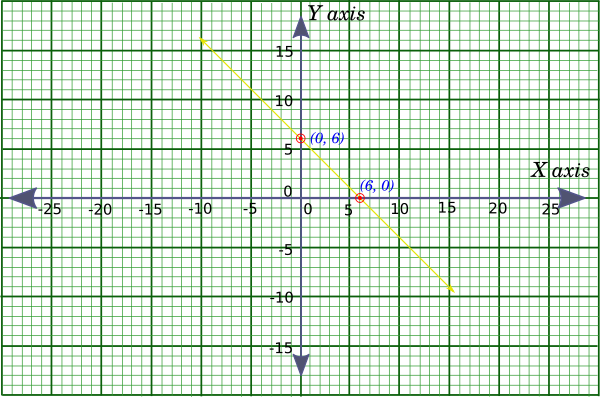
In our case, if we put $x = 0$, we get $y = 6$, therefore, the point $(0,\ 6)$ satisfies the given equation.

Again, putting $y = 0$ we get $x = 6$, therefore the point $(6,\ 0$ also satisfies the given equation.

Hence, if we plot these two points on the Cartesian plane, then join the two points and extend the line on both sides, we will get our required line.

-----------book page break-----------

If you plot the line correctly it would look like the figure below. The two plotted points are shown using red dots, and the line is shown in yellow.

Remember, this approach will not work for lines passing through the origin which are of the form $y = ax$. Since the line passes through the point $(0, 0)$ putting $x = 0$ or $y = 0$ will give us the same point $(0,\ 0)$ and it will not be possible to draw a unique line through it. It that case, the first point can be $(0,\ 0)$ and for the second point we have to select a non-zero value of $x$ to get two distinct points.