Pythagoras Theorem

One of the most well known and oldest theorem in mathematics is the Pythagoras theorem. It states that the square drawn on the hypotenuse of a right angled triangle is equal to the sum of the squares drawn on the remaining two sides. That is, if we have a right angled triangle whose sides are $a$, $b$ and $c$ where $c$ is the hypotenuse, then:

$a^2 + b^2 = c^2$

$\underline{Some\ Interesting\ Facts\ About\ Pythagoras\ Theorem}$

This theorem was discovered many years before Pythagoras, in around $1900\ BC$. Pythagoras was the first to prove this theorem in around $500\ BC$.
Since then, many people have provided different proofs of this theorem, including one from famous mathematician $Euclid$ and another from $J.A.\ Garfield$, an American president.

Today we will see one of the simpler proofs which will be easy to understand.

-----------book page break-----------

Let us take a right angled triangle $ABC$, with $\angle ACB = 90^o$, which means $AB$ is the hypotenuse. We will need to prove that $AB^2 = BC^2 + CA^2$

$\underline{Construction}$

Draw a square on the side $AB$ and call it $BAPQ$

From point $P$ draw a perpendicular to extended $CA$ at $D$, similarly from point $Q$ draw a perpendicular to extended $DP$ at $E$ and from point $B$ draw a perpendicular to extended $EQ$ at $F$.

We get the figure below.

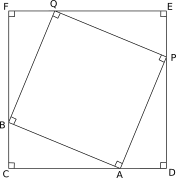
$\underline{Proof}$

Consider $\triangle s$ $ABC$ and $PAD$

$\angle CAB + \angle CBA = 90^o$

$\angle CAB + \angle PAD = 180^o - 90^o = 90^o$

$\texttip{\therefore}{therefore} \angle CBA = \angle PAD$

$AB = AP$, $\texttip{\because}{because} BAPQ$ is a square

$\angle BCA = \angle ADP$ $\texttip{\because}{because}$ both are right angles

$\texttip{\therefore}{therefore} \triangle ABC \texttip{\cong}{congruent to} \triangle PAD$ $(AAS$ rule$)$

$\texttip{\therefore}{therefore} AD = BC, and AC = PD$

$CD = CA + AD = CA + BC$

-----------book page break-----------

Similarly, we can show that

$FQ = EP = AD = BC$ and $FB = EQ = PD = AC$

$\texttip{\therefore}{therefore} CDEF$ is a square with each of its side $= BC + CA$

Area of $CDEF = (BC + CA)^2$

Area $\triangle ABC = $ Area $\triangle ADP$ = Area $\triangle PEQ$ = Area $\triangle QFB$ = $\dfrac{1}{2} \times BC \times CA$

Area of $BAPQ = AB^2$

We know that,

Area of $BAPQ =$ Area of $CDEF - ($ Area $\triangle ABC + $ Area $\triangle ADP$ + Area $\triangle PEQ$ + Area $\triangle QFB)$

$\texttip{\Rightarrow}{follows that} AB^2 = (BC + CA)^2 - 4 \times \left(\dfrac{1}{2} \times BC \times CA\right)$ $\texttip{\because}{because}$ Each of these triangles has an area of $\dfrac{1}{2} \times BC \times CA$

$\texttip{\Rightarrow}{follows that} AB^2 = (BC + CA)^2 - 2 \times BC \times CA$

$\texttip{\Rightarrow}{follows that} AB^2 = BC^2 + CA^2 + 2 \times BC \times CA - 2 \times BC \times CA$

$\texttip{\therefore}{therefore} AB^2 = BC^2 + CA^2$