Ptolemy's Theorem

$\underline{Theorem:}$

Ptolemy's theorem states that for any cyclic quadrilateral $ABCD$, the product of the two diagonals is equal to the sum of the product of each pair of opposite sides, that is, for a cyclic quadrilateral $ABCD$:

$AC \times BD = AB \times CD + BC \times DA$

$\underline{Construction:}$

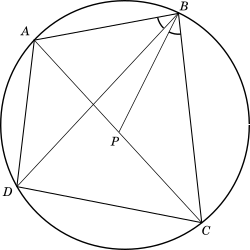
We draw the cyclic quadrilateral $ABCD$ as shown in the figure below. From the vertex $B$ we draw a line to meet the dia, such that $\angle CBP = \angle ABD$

-----------book page break-----------

$\underline{Proof:}$

$\angle ACD = \angle ABD$ since they are angles subtended by the same arc $AD$ at the circumference.

$\angle BCP = \angle BDA$

$\angle PBC = \angle DBA$

$\therefore \triangle BCP \sim \triangle BDA$

$\therefore \dfrac{BC}{DB} = \dfrac{PC}{AD}$

$\Rightarrow BC \times AD = PC \times DB$ $...eqn\ (i)$

$\angle PBA = \angle DBA + \angle PBD$

$\angle DBC = \angle PBC + \angle PBD$

$\angle PBC = \angle DBA$

$\therefore \angle DBA + \angle PBD = \angle PBC + \angle PBD$

$\therefore \angle PBA = \angle DBC$

Also,

$\angle CDB = \angle CAB$

$\therefore \triangle CDB \sim \triangle PAB$

$\therefore \dfrac{AB}{BD} = \dfrac{AP}{CD}$

$\Rightarrow AB \times CD = AP \times BD$ $...eqn\ (ii)$

Adding this with $eqn\ (i)$ and $eqn\ (ii)$ we get:

$BC \times AD + AB \times CD = PC \times DB + AP \times BD$

$\Rightarrow BC \times AD + AB \times CD = (PC + AP) \times BD$

$\Rightarrow BC \times AD + AB \times CD = AC \times BD$

$\therefore AC \times BD = AB \times CD + BC \times DA$