Basic Definitions In Geometry - Angles & Polygons

I. Angles

Angles are used to measure the rotation of one line with respect to a fixed line. One of the units used commonly to express angles is called $degree$ written as $^o$. There are other units as well, like $radians$ written as $^c$ which is widely used in science and $gradian$ written as $^g$ which is rarely used anywhere.

Imagine a clock with fixed line $OA$ drawn from the centre $O$ to the $12\ o'clock$ position $A$ and $OB$ as the minute hand, as shown in the figure below:

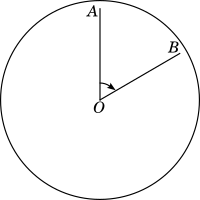
After some time the minute hand would have rotated about the point $O$ and reached the position shown in the figure above. We can measure this rotation of the minute hand using angle.

-----------book page break-----------

In one hour the minute hand rotates by one complete rotation starting at the fixed line and coming back to the same line as shown below:

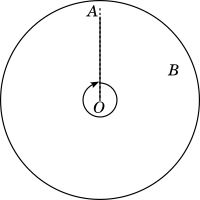
The measure of this complete rotation is taken as $360^o$ (in degrees) or $2\pi^c$ (in radians) or $400^g$ (in gradians). We will cover $\pi$ and $radians$ at a higher grade. For now we will focus only on degrees.

II. Types Of Angles

An angle which is less than $90^o$ is called an

$accute\ angle$

An angle which is equal to $90^o$ is called a

$right\ angle$

An angle which is greater than $90^o$ but less than $180^o$ is called an

$obtuse\ angle$

An angle which is equal to $180^o$ is called a

$straight\ angle$

An angle which is greater than $180^o$ but less than $360^o$ is called a

$reflex\ angle$

-----------book page break-----------

III. Naming An Angle

An angle is denoted using the symbol $\angle$ followed by the name of the angle, denoted by three alphabets.

You need to make sure that the point of rotation is always the middle letter of the angle name.

For example the angle shown below should be called $\angle PQR$, calling it $\angle PRQ$ or $\angle RPQ$ would be incorrect.

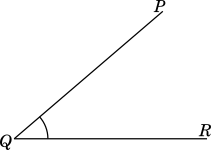
In some cases, it is acceptable to name an angle with just the single letter which is the point of rotation of the two lines, for example the angle shown above can also be called $\angle Q$

-----------book page break-----------

IV. Polygons

Polygons are figures bounded by $3$ or more straight lines, which is closed. For example, in the following figure, $PQRST$ is a $5$ sided polygon, whereas $ABCDE$ is $NOT$ a polygon because it is not closed.

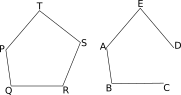
Polygons with smaller number of sides have specific names. Following is a list of polygons with up to $12$ sides and their names:

$3$ sided polygon -

$triangle$

$4$ sided polygon -

$quadrilateral$

$5$ sided polygon -

$pentagon$

$6$ sided polygon -

$hexagon$

$7$ sided polygon -

$heptagon$

$8$ sided polygon -

$octagon$

$9$ sided polygon -

$nonagon$

$10$ sided polygon -

$decagon$

$11$ sided polygon -

$hendecagon$

$12$ sided polygon -

$dodecagon$

-----------book page break-----------

V. Regular Polygons

A polygon with all of its sides equal to one another and angles equal to one another is called a regular polygon.

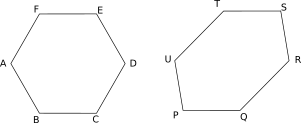
In the figure shown above, $ABCDEF$ is a regular hexagon since all of its sides are equal and so are the angles, but $PQRSTU$ is not a regular hexagon even though all the sides are equal. This is because the angles of $PQRSTU$ are not equal.

VI. Convex Polygons

Convex polygons are polygons with all of its angles less than $180^o$. All the polygons shown so far in our examples are convex polygons.

VII. Concave Polygons

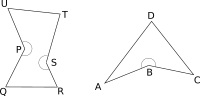
Concave polygons are polygons with one or more of its angles greater than $180^o$

-----------book page break-----------

In the figure above $PQRSTU$ is a concave hexagon and $ABCD$ is a concave quadrilateral. All the angles that are more than $180^o$ are marked.

We will learn more about properties of polygons later.

Points, Lines & Planes