Trigonometric Ratios Of Common Angles & Their Derivations
Today we will see how to derive the trigonometric ratios of common common angles. We will start with the angles $30^\circ$, $45^\circ$ and $60^\circ$. And then we will cover the special cases of $0^\circ$ and $90^\circ$.
$\underline{I.\ Trigonometric\ Ratios\ of\ 30^\circ\ \&\ 60^\circ\ Angles}$
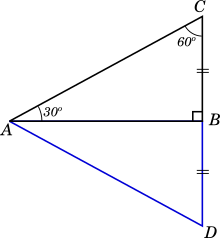
Let us take right triangle $ABC$ with $\angle ABC = 90^\circ$ and $\angle BAC = 30^\circ$. Therefore, $\angle BCA = 90 - 30 = 60^\circ$.
Let us do the following constructions:
- Extend side $CB$ to point $D$ such that $BD = BC$.
- Join points $A$ and $D$.
The diagram is provided below, with the construction lines shown in blue:
-----------book page break-----------
In $\triangle ABD$ $\angle ABD = 180 - 90 = 90^\circ$
Consider triangles $ABC$ and $ABD$.
$BC = BD$ (by construction)
$\angle ABC = \angle ABD$ (both are $90^\circ$)
$AB$ is common.
$\therefore \triangle ABC \cong \triangle ABD$
$\therefore \angle D = 60^\circ$
$\angle BAD = \angle BAC = 30^\circ$
$\angle DAC = 30 + 30 = 60^\circ$, and $\triangle ADC$ is an equilateral triangle, with $B$ as the midpoint of $DC$
$\therefore BC = \dfrac{1}{2}DC = \dfrac{1}{2}AC$
Let us take the length of the hypotenuse $AC$ as $h$
$\therefore BC = \dfrac{h}{2}$
We can find the length of $AC$ using the Pythagoras theorem applied to right angled $\triangle ABC$
$AB^2 + BC^2 = AC^2$
$\Rightarrow AB^2 + \left(\dfrac{h}{2}\right)^2 = h^2$
$\Rightarrow AB^2 = h^2 - \left(\dfrac{h}{2}\right)^2$
$\Rightarrow AB = \sqrt{h^2 - \left(\dfrac{h}{2}\right)^2}$
-----------book page break-----------
$\Rightarrow AB = \sqrt{h^2 - \dfrac{h^2}{4}}$
$\Rightarrow AB = \sqrt{\dfrac{4h^2 - h^2}{4}}$
$\Rightarrow AB = \sqrt{\dfrac{3h^2}{4}}$
$\Rightarrow AB = \dfrac{\sqrt{3}}{2}h$
Now that we know that $AC = h$, $BC = \dfrac{h}{2}$ and $AB = \dfrac{\sqrt{3}\ h}{2}$ ,we can find all the trigonometric ratios for the angles $30^\circ$ and $60^\circ$
$sin(30^\circ) = \dfrac{BC}{AC} = \dfrac{\frac{h}{2}}{h} = \dfrac{h}{2} \times \dfrac{1}{h} = \dfrac{1}{2}$
$sin(60^\circ) = \dfrac{AB}{AC} = \dfrac{\frac{\sqrt{3}\ h}{2}}{h} = \dfrac{\sqrt{3}\ h}{2} \times \dfrac{1}{h} = \dfrac{\sqrt{3}}{2}$
We can find out $cos(30^\circ)$ and $cos(60^\circ)$ in the same way, but since we learnt about ratios of complementary angles , we will use that instead, just for fun:
$cos(30^\circ) = cos(90 - 60) = sin(60^\circ) = \dfrac{\sqrt{3}}{2}$ (we know that $cos(90 - \theta) = sin(\theta)$)
$cos(60^\circ) = cos(90 - 30) = sin(30^\circ) = \dfrac{1}{2}$
-----------book page break-----------
$tan(30^\circ) = \dfrac{BC}{AB} = \dfrac{\frac{h}{2}}{\frac{\sqrt{3}\ h}{2}} = \dfrac{h}{2} \times \dfrac{2}{\sqrt{3}\ h} = \dfrac{1}{\sqrt{3}}$
$tan(60^\circ) = \dfrac{AB}{BC} = \dfrac{\frac{\sqrt{3}\ h}{2}}{\frac{h}{2}} = \dfrac{\sqrt{3}\ h}{2} \times \dfrac{2}{h} = \sqrt{3}$
Now we have more than one ways to find out the remaining ratios, $cosec$, $sec$ and $cot$ of these angles. We will use the inverse relationship from to find these ratios:
$cosec(30^\circ) = \dfrac{1}{sin(30^\circ)} = \dfrac{1}{\frac{1}{2}} = 2$
$cosec(60^\circ) = \dfrac{1}{sin(60^\circ)} = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}$
$sec(30^\circ) = \dfrac{1}{cos(30^\circ)} = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}$
$sec(60^\circ) = \dfrac{1}{cos(60^\circ)} = \dfrac{1}{\frac{1}{2}} = 2$
$cot(30^\circ) = \dfrac{1}{tan(30^\circ)} = \dfrac{1}{\frac{1}{\sqrt{3}}} = \sqrt{3}$
$cot(60^\circ) = \dfrac{1}{tan(60^\circ)} = \dfrac{1}{\sqrt{3}}$
-----------book page break-----------
$\underline{II.\ Trigonometric\ Ratios\ of\ 45^\circ\ Angle}$
We will start by taking a $\triangle ABC$ with $\angle ABC = 90^\circ$ and $\angle BAC = 45^\circ$ as shown below:
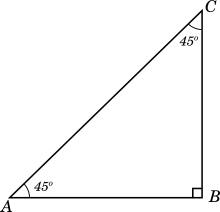
$\angle BCA = 90 - 45 = 45^\circ$
$\therefore \triangle ABC$ is an isosceles triangle with $BA = BC$
Like before, let us take the length of the hypotenuse as $h$, and apply Pythagoras theorem on this right angled triangle:
$AB^2 + BC^2 = AC^2 = h^2$ since $BC = AB$ we can replace $BC$ with $AB$ and get:
$AB^2 + AB^2 = h^2$
$\Rightarrow 2AB^2 = h^2$
$\Rightarrow AB^2 = \dfrac{h^2}{2}$
-----------book page break-----------
$\Rightarrow AB = \dfrac{h}{\sqrt{2}}$
Therefore, we have $AC = h$, $AB = BC = \dfrac{h}{\sqrt{2}}$, and we are ready to find out all the trigonometric ratios for $\angle A = 45^\circ$
$sin(45^\circ) = \dfrac{BC}{AC} = \dfrac{\frac{h}{\sqrt{2}}}{h} = \dfrac{1}{\sqrt{2}}$
$cos(45^\circ) = \dfrac{AB}{AC} = \dfrac{\frac{h}{\sqrt{2}}}{h} = \dfrac{1}{\sqrt{2}}$
$tan(45^\circ) = \dfrac{BC}{AB} = \dfrac{\frac{h}{\sqrt{2}}}{\frac{h}{\sqrt{2}}} = 1$
We can find the remaining ratios using the inverse relationships from .
$cosec(45^\circ) = \dfrac{1}{sin(45^\circ)} = \dfrac{1}{\frac{1}{\sqrt{2}}} = \sqrt{2}$
$sec(45^\circ) = \dfrac{1}{cos(45^\circ)} = \dfrac{1}{\frac{1}{\sqrt{2}}} = \sqrt{2}$
$cot(45^\circ) = \dfrac{1}{tan(45^\circ)} = \dfrac{1}{1} = 1$
-----------book page break-----------
$\underline{III.\ Trigonometric\ Ratios\ of\ 0^\circ\ \&\ 90^\circ\ Angles}$
So far we have been using right triangles with another angle as the $\theta$ value to find the trigonometric ratios for $\theta$.
Unfortunately, we cannot have a triangle with $0^\circ$ angle or a right triangle with another of its angles as $90^\circ$
Instead, we will use something called the $unit\ circle$ to find the trigonometric ratios for $0^\circ$ and $90^\circ$
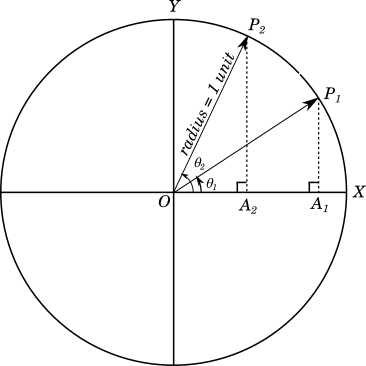
We have taken a circle with centre $O$ and a radius of $1$ unit, as shown below:
-----------book page break-----------
We have taken a radius of the circle which is rotating about the centre $O$ and we have shown two random positions $1$ and $2$ of the radius at angles $\theta_1$ and $\theta_2$, and touching the circle at points $P_1$ and $P_2$ respectively.
At each of these positions we have drawn a perpendicular from point $P_i$ to a point $A_i$ on the line $OX$.
Now we have our right triangle for each of $\theta_i$ as $P_iA_iO$ and we can find the trigonometric ratios of $\theta_1$ and $\theta_2$ using the triangles $P_1A_1O$ and $P_2A_2O$
For example $sin(\theta_1) = \dfrac{P_1A_1}{P_1O} = \dfrac{P_1A_1}{r} = \dfrac{P_1A_1}{1} = P_1A_1$ (we took the radius of this circle as $1$ unit), and
$sin(\theta_2) = \dfrac{P_2A_2}{P_2O} = \dfrac{P_2A_2}{r} = \dfrac{P_2A_2}{1} = P_2A_2$
Now let's see when $\theta$ becomes close to $0^\circ$. Both the point $P$ and $A$ approaches point $X$, and when $\theta$ becomes exactly $0$, the three points $P$, $A$ and $X$ coincide.
At that point $OA = OX = r$ and $PA = 0$
Therefore, $sin(0^\circ) = \dfrac{PA}{r} = \dfrac{0}{r}$
$cos(0) = \dfrac{OA}{OP} = \dfrac{r}{r} = 1$
$tan(0) = \dfrac{PA}{OA} = \dfrac{0}{r} = 0$
We can find the remaining ratios by taking the inverses of the above three ratios.
$cosec(0) = \dfrac{1}{sin(0)} = \dfrac{1}{0} = undefined$
$sec(0) = \dfrac{1}{cos(0)} = \dfrac{1}{1} = 1$
$cot(0) = \dfrac{1}{tan(0)} = \dfrac{1}{0} = undefined$
-----------book page break-----------
Finally, we will summarise the values of all the trigonometric ratios of all the common angles below:
| $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | |
| $sin$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | $1$ |
| $cos$ | $1$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{2}$ | $0$ |
| $tan$ | $0$ | $\dfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | $undefined$ |
| $cosec$ | $undefined$ | $2$ | $\sqrt{2}$ | $\dfrac{2}{\sqrt{3}}$ | $1$ |
| $sec$ | $1$ | $\dfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | $2$ | $undefined$ |
| $cot$ | $undefined$ | $\sqrt{3}$ | $1$ | $\dfrac{1}{\sqrt{3}}$ | $1$ |