We learnt about simple algebraic identities hereSimple Algebraic Identities. Today we are going to see more generic cases of algebraic identities.

Very specifically we will learn the generic method to expand the following expressions:

$(a + b)^n$

$(a - b)^n$,

and the factorisation of:

$a^n + b^n$

$a^n - b^n$

We need to understand that the expansion of $(a \pm b)^n$ is usually done using the concept of combination and factorials.

However, since we are learning these expansions before we have learnt permutation/combination, we will use another trick called $Pascal's\ Triangle$ to find the expansions of these expressions.

Look at the figure below:

             

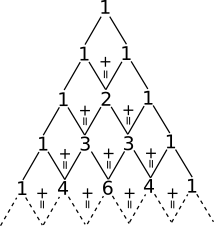
In $Pascal's\ Triangle$ the row count starts from the top, with the topmost row as the $0\raise{0.3em}{\underline{th}}$ row. The top row (or the $0\raise{0.3em}{\underline{th}}$ row) of a $Pascal's\ Triangle$ contains a single number, $1$. Numbers in every subsequent row consists of numbers which are sum of the two adjacent numbers from the previous row. For example, the $3$ in the third row is obtained by adding the adjacent $2$ and $1$ from the second row. The numbers on the edge has only one adjacent number in the previous row, it is just equal to that number.

The second row therefore contains the numbers $1$ and $1$.

The third row contains $1$, $2$ $(1 + 1 = 2)$ and $1$ and the fourth row contains $1$, $3\ (1 + 2 = 3)$, $3\ (2 + 1 = 3)$ and $1$. Likewise the $Pascal's\ Triangle$ can be extended up to infinite number of rows.

Now let's look at how $Pascal's\ Triangle$ can be used to find the expanded form of $(a + b)^n$.

Each of the rows in the $Pascal's\ Triangle$ corresponds to the coefficients of $(a + b)^n$, starting with $n = 0$.

Notice here, that the expansion of $(a + b)^n$ will contain $n + 1$ terms.

For, $n = 0$ we have

$(a + b)^0 = 1$    (contains $1$ term)

Here there is a single terms, which is corresponding to the $0\raise{0.3em}{\underline{th}}$ row of the $Pascal's\ Triangle$

For $n = 1$

$(a + b)^1 = a + b$     (contains $2$ terms)

The coefficients are $1$ and $1$ which correspond to the $1\raise{0.3em}{\underline{st}}$ row of the $Pascal's\ Triangle$

For $n = 2$

$(a + b)^2 = a^2 + 2ab + b^2$      (contains $3$ terms)

The coefficients are $1$, $2$ and $1$ which correspond to the $2\raise{0.3em}{\underline{nd}}$ row of the $Pascal's\ Triangle$

Likewise, for $n = 3$, we take the third row of the $Pascal's\ Triangle$ which has $1,\ 3,\ 3,\ 1$

$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$

Thus, we can get the coefficients of any binomial expansion of the form $(a + b)^n$ using the $Pascal's\ Triangle$.

How to get the variables for each of these terms? It is easy. The first term always contains $a^n$ which is same as $a^nb^0$. For each subsequent term, the power of $a$ is reduced by $1$ and the power of $b$ is increased by $1$.

The second term will contain $a^{n-1}b$, the third term will contain $a^{n-2}b^2$ till the power of $a$ reaches $0$ and the power of $b$ reaches $n$.

Following this method, we can find the expansion of $(a + b)^4$.

The fourth row of the $Pascal's\ Triangle$ contains the numbers $1,\ 4,\ 6,\ 4,\ 1$ which will be the coefficients for this expansion. The variables for each of the terms will go like $a^4$, $a^3b$, $a^2b^2...$ $b^4$.

Hence our final expansion will be

$(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4$

Now we will see how to expand an expression of the form $(a - b)^n$.

Once we have understood the expansion of $(a + b)^n$, it becomes very easy to extend it to $(a - b)^n$

We can write $(a - b)^n$ as $\{a + (-b)\}^n$ and use our previous knowledge to expand this.

$\{a + (-b)\}^n = C_0a^n + C_1a^{n-1}(-b) + C_2a^{n-2}(-b)^2.... + C_n(-b)^n$, where $C_0... C_n$ are coefficients of the respective terms.

We also know that an even power of a negative number is positive and an odd power of a negative number is negative.

For example, $(-b)^1 = -b$, $(-b)^2 = b^2$, $(-b)^3 = -b^3$ and so on.

Hence in our expansion, every odd power of $b$ will be a negative number will be negative, and every even power of $b$ will be a positive term.

We can take the examples of $(a - b)^3$ and $(a - b)^4$ to understand this better.

$(a - b)^3$

$= \{a + (-b)\}^3$

$= a^3 + 3a^2(-b) + 3a(-b)^2 + (-b)^3$

$= a^3 - 3a^2b + 3ab^2 - b^3$

Similarly for $(a - b)^4$, we get

$(a - b)^4$

$=\{a + (-b)\}^4$

$= a^4 + 4a^3(-b) + 6a^2(-b)^2 + 4a(-b)^3 + (-b)^4$

$= a^4 - 4a^3b + 6a^2b^2 - 4ab^3 + b^4$

Note: When you are using $Pascal's\ Triangle$ to expand $(a \pm b)^n$ there is an obvious disadvantage that you need to construct the triangle till the $n\raise{0.2em}{th}$ row which means finding all rows till $n$. This makes this method unsuitable for use with larger values of $n$. We will learn more efficient method at a higher grade which uses $combinations$.

Let us try this problem before we move on to the next section.

Now we will look at the factorisation of $a^n + b^n$ and $a^n - b^n$

Factorisation of $a^n + b^n$ exists only for odd values of $n$ but doesn't exist for even values of $n$, whereas,

factorisation of $a^n - b^n$ exist for both odd and even values of $n$

For odd values of $n$

$a^n + b^n = (a + b)\{a^{n-1} - a^{n-2}b + a^{n-3}b^2... +b^{n-1}\}$

We will illustrate this by expanding $a^3 + b^3$ and $a^5 + b^5$

$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$

$a^5 + b^5 = (a + b)(a^4 - a^3b + a^2b^2 - ab^3 + b^4)$

Factorisation of $a^n - b^n$ for either odd or even $n$ is of the form:

$a^n - b^n = (a-b)(a^{n-1} + a^{n-2}b + a^{n-3}b^2 ... + b^{n-1})$

We will see a few examples to understand this form of expansion better:

$a^2 - b^2 = (a - b)(a + b)$

$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$

$(a^4 - b^4) = (a - b)(a^3 + a^2b + ab^2 + b^3)$

$(a^5 - b^5) = (a - b)(a^4 + a^3b + a^2b^2 + ab^3 + b^4)$