Sum Of Angles Of A Triangle

Theory

The sum of the three internal angles of a triangle is $180^o$.

Contstruction

Let us draw any triangle $\triangle ABC$, and extend the side $BC$ to $D$ and draw a line $CE$ parallel to $BA$ and passing through $C$, as shown in the figure below.

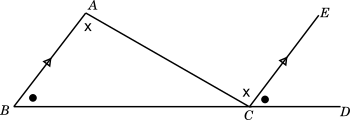
Proof

We need to prove that the three internal angles of $\triangle ABC$, $\angle ABC + \angle BAC + \angle BCA = 180^o$

We know that $CE \parallel BA$

Considering $AC$ as the transversal, $\angle BAC = $

$\angle ACE$

, since they are alternate interior angles..

Considering $BD$ as the transversal, $\angle ABC =$

$\angle ECD$

, since they are corresponding angles.

(You can refer to the properties of parallel lines and transversals )

-----------book page break-----------

As $BD$ is a straight line $\angle BCA + \angle ACE + \angle ECD =$

$180^o$

Now replacing $\angle ACE$ with $\angle BAC$ and $\angle ECD$ with $\angle ABC$ because they are equal, we get:

$\angle BCA + \angle BAC + \angle ABC = 180^o$

Therefore, the sum of the three internal angles of the given triangle $180^o$