Catalan Numbers
I. Introduction
Catalan numbers are an important concept in combinatorics and can be used to solve a variety of counting problems.
II. Derivation
We will understand the derivation of the expression using a well known problem called the parenthesization problem.
This problem involves counting the number of valid arrangements of $n$ opening parenthesis and $n$ closing parenthesis.
For example when we have $1$ each of opening and closing parenthesis, we have just $1$ valid arrangement, which is:
$()$ and the other possible arrangement $)($ is invalid.
Similarly with $2$ opening and $2$ closing parenthesis the valid arrangements are:
$(())$ and $()()$.
It is easy to see that any valid arrangement of a set of $2n$ parenthesis will need to fulfill one condition, that is is at no point in an arrangement the count of closing parenthesis can exceed the count of opening parenthesis till that point.
Without any restriction, it is possible to have $\dfrac{2n!}{n! n!} = \xacomb{2n}{n}$ arrangements with $n$ opening and $n$ closing parenthesis.
Now we can derive the expression for the count of valid arrangement by counting the number of invalid arrangements and subtracting them from the number of total arrangements.
-----------book page break-----------
We can see that for every invalid arrangement, there is a position $k$ where the number of closing parenthesis exceeds the number of opening parenthesis for the first time. Therefore, till position $k - 1$ there is an equal number of opening and closing parenthesis, and hence $k-1$ is even and $k$ is odd. Till the position $k$ there is one closing parenthesis more than the number of opening parenthesis. Therefore, of the remaining $2n - k$ parenthesis there is one opening parenthesis more than the closing parenthesis. Now, if we interchange the opening and closing parenthesis in the remaining, in all we will have a total of $n - 1$ opening parenthesis and $n + 1$ closing parenthesis.
Given a system of $2n$ parentheses with $n-1$ opening and $n+1$ closing parentheses it is impossible to have a valid parenthesization and any arrangement of these parenthesis will always be imbalanced. Every arrangement of $n-1$ opening and $n+1$ closing parenthesis can be swapped in the previous way to obtain an invalid arrangement of $n$ opening and $n$ closing parenthesis, similarly every invalid arrangement of $n$ opening and $n$ closing parentheses can be mapped to an arrangement of $n-1$ opening and $n+1$ closing parentheses.
Since there is a clear bijection between the two, the number of invalid arrangements with $n$ opening and $n$ closing parentheses is equal to the total number of arrangements of $n-1$ opening and $n+1$ closing parenthesis, which is given by $\dfrac{2n!}{(n-1)! (n+1)!}$
Therefore the number of valid arrangements is:
$\dfrac{2n!}{n! n!} - \dfrac{2n!}{(n-1)! (n+1)!}$
$= \dfrac{1}{n+1} \left( \xacomb{2n}{n} \right)$
-----------book page break-----------
III. Understanding Using Recurrence
In the previous section we saw a closed form for the $n \xasuper{th}$ Catalan Number. In this section we will see a recurrence relation which will allow us to compute the $(n+1) \xasuper{th}$ Catalan number using the previous Catalan numbers upto $n$.
We will use the parenthesization problem from the previous section to understand the recurrence relation.
Let us consider the base cases first.
We take the Catalan number $C_0$ as $1$, because there is only one arrangement using $0$ parentheses, that is the null arrangement.
With $n = 1$ we can have only $1$ valid arrangement, which is $()$
With $n = 2$, we have two valid arrangements, which are $()()$ and $(())$
To understand the recurrence relation, we will consider $C_3$. Let's say, the number of possible arrangements with $n = 0, 1, 2$ are denoted by $C_0, C_1, C_2$ respectively.
When we introduce two new parenthesis in an arrangement of $2$ pairs of parentheses, we can do it by dividing any arrangement of $2$ pairs of parentheses into two groups $AB$ such that $A + B = 2$ for all $A, B$ and then enclose $A$ with the new pair of parentheses. So our arrangement becomes $(A)B$.
The following table shows the possible arrangements using this recurrence method. The pair of parentheses in blue shows the positions we are introducing the third pair of parenthesis.
| $A$ | $B$ | $Count$ | $Arrangements$ ${\color{blue}(} A {\color{blue})}B$ |
| $0$ | $2$ | $C_0 \cdot C_2 = 1 \cdot 2 = 2$ | $\Large {\color{blue}()} ()()$, $\Large {\color{blue}()}(())$ |
| $1$ | $1$ | $C_1 \cdot C_1 = 1 \cdot 1 = 1$ | $\Large {\color{blue}(} () {\color{blue})}()$ |
| $2$ | $0$ | $C_2 \cdot C_0 = 2 \cdot 1 = 2$ | $\Large {\color{blue}(} ()() {\color{blue})}$, $\Large {\color{blue}(} (()) {\color{blue})}$ |
Therefore, $C_3 = C_0 \cdot C_2 + C_1 \cdot C_1 + C_2 \cdot C_0 = 2 + 1 + 2 = 5$
-----------book page break-----------
In general for any $n \ge 2$, we have:
$C_n = \displaystyle \sum\limits_{i = 0}^{n-1} C_{i} \cdot C_{n-i-1}$
IV. Common Problems
In general any problem that involves arranging two sets each of $n$ identical elements, such that the total count of one element from the left never exceeds the count of the other element, can be mapped directly to the Catalan Number $C_n$.
Here are a few well known problems which are often used to demonstrate the Catalan Number problem.
$\underline{\text{A. The Grid Walking Problem}}$
This problem involves walking along a path in an $n \times n$ square grid, such that the path never crosses the diagonal line (it can touch the diagonal, though).
-----------book page break-----------
The figure below shows a $9 \times 9$ such grid. The path in red is an example of an invalid path because it crosses the blue diagonal line. The path in green is a valid path, because it doesn't cross the diagonal.
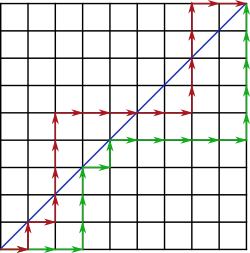
It is evident that the minimum path from the bottom left corner to the top-right corner will have $9$ right moves and $9$ up moves. Whenever there is a point where the number of up moves exceed the number of right moves, the path will cross the diagonal. If a path maintains $\text{up moves} \le \text{right moves}$ at all points, then it gives us a valid path.
This a straight mapping to our parenthesization problem, where any valid path will have less than or equal number of closing parenthesis as the opening parenthesis.
This a straight mapping to our parenthesization problem, where any valid path will have less than or equal number of closing parenthesis as the opening parenthesis.
-----------book page break-----------
$\underline{\text{B. Polygon Triangulation Problem}}$
Given a polygon of $n + 2$ sides, how many ways are there to divide the polygon into triangles by joining the vertices, without any any sides intersecting each other.
The diagram below shows two possible triangulation of a hexagon.
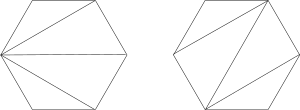
It can be shown that total number of triangulation arrangement for a $n + 2$ sided polygon is the $n\xasuper{th}$ Catalan number $C_n$. We will leave the proof of this to the reader. This can be easily mapped to the recurrence approach described in $Section\ II$.
$\underline{\text{C. Rooted Binary Trees}}$
A rooted binary tree is a tree where every node has $0, 1$ or $2$ child edges, and a node with a left child is distinct from a node with a right child.
The number of possible trees with $n$ edges is given by $C_{n}$.
This problem has a simple and straightforward mapping with the recurrence proof of the Catalan Number, therefore, we will leave it to the reader to figure out the mapping.
Introduction To Permutation -
Introduction To Combination -