Secant Theorem

$\underline{Theorem}$

The secant theorem states that for two non-parallel secants $AB$ and $CD$ intersecting at point $P$, either inside or outside the circle, the relationship:

$\overline{PA} . \overline{PB} = \overline{PC} . \overline{PD}$

$\underline{Construction}$

We will draw two figures for this theorem, in the first case the secants meet at point $P$ external to the circle, and in the second case they intersect at point $P$ which is internal to the circle. In both cases lines $BD$ and $AC$ are joined. Both figures are shown below:

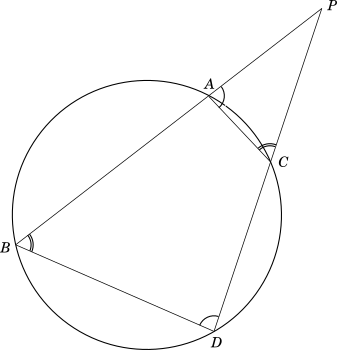
$Figure-1$

-----------book page break-----------

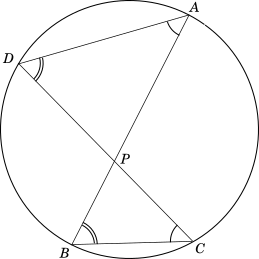
$Figure-2$

$\underline{Proof}$

In $Fig.\ 1$, $\angle BDC + \angle BAC = 180^\circ$ and $\angle PAC + \angle BAC = 180^\circ$

$\therefore \angle BDC = \angle PAC$

Similarly,

$\angle DBA = \angle PCA$

$\therefore \triangle PCA \sim \triangle PBD$

In $Fig.\ 2$,

$\angle PAC = \angle PDB$

$\angle PBD = \angle PCA$

Therefore, $\triangle PCA \sim \triangle PBD$

-----------book page break-----------

Therefore, in both the cases corresponding sides are in proportion, that is:

$\dfrac{PA}{PD} = \dfrac{PC}{PB}$

$\overline{PA}.\overline{PB} = \overline{PC}.\overline{PD}$

$\underline{Corollary\ 1}$

If a secant $AB$ to a circle meets a tangent $PT$ to the circle at point $P$, then:

$\overline{PA}.\overline{PB} = \overline{PT}^2$

It is easy to see from $Fig.\ 1$ that if you rotate $PD$ about point $P$ such that it becomes a tangent to the given circle, points $C$ and $D$ coincide at $T$, the point of tangent, and $PC$ and $PD$ become equal to $PT$, therefore,

$\overline{PA}.\overline{PB} = \overline{PT}^2$

We will also see a different approach to this proof below.

We will draw a circle with a point $P$ external to it. From $P$ we will draw a secant $PB$ to intersect the circle at $A$ and $B$ and a tangent $PT$ touching the circle at $T$, as shown below:

-----------book page break-----------

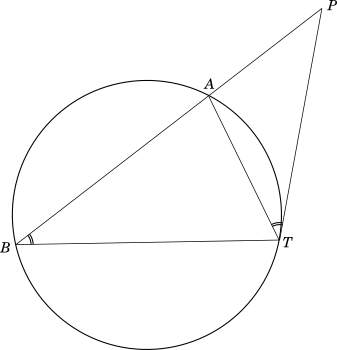
Considering $\triangle s\ PTA$ and $PBT$,

$\angle P$ is common.

$\angle TBP = \angle ATP$ (angles in alternate segment, as proven .)

Therefore,

$\triangle PTA \sim \triangle PBT$

Therefore,

$\dfrac{PA}{PT} = \dfrac{PT}{PB}$

$\Rightarrow \overline{PA}.\overline{PB} = \overline{PT}^2$