Trigonometric Ratios Of Compound Angles

In this chapter we will learn about trigonometric ratios of compound angles (of the form $A \pm B$) and their derivations.

I. Evaluating sin(A ± B):

We draw the diagram for our proof as follows.

Draw $\angle AOB$ such that $m\angle AOB = A$ and $\angle BOC$ such that $m\angle BOC = B$. From any point $P$ on $CO$ drop perpendiculars $PM$ and $PN$ to $AO$ and $BO$ respectively. From $N$ draw perpendiculars $NQ$ and $NR$ to $AO$ and $PM$ respectively, as shown in the following diagram:

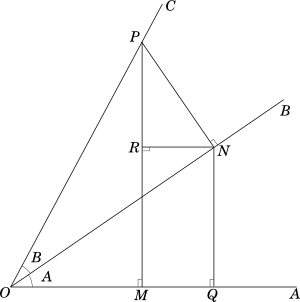
$Fig.\ 1$

-----------book page break-----------

$\angle NRM = \angle RMQ = 90^\circ$

Therefore, $NRMQ$ is a rectangle with $NR \parallel QM \therefore NR \parallel OA$

$\therefore \angle AOB = \angle RNO = A$

$\angle RPN = 90^\circ - \angle PNR = \angle RNO = A$

$\sin(A + B) = \dfrac{PM}{OP} = \dfrac{RM + PR}{OP}$

$= \dfrac{RM}{OP} + \dfrac{PR}{OP}$

$= \dfrac{NQ}{OP} + \dfrac{PR}{OP}$

$= \dfrac{NQ \times ON}{ON \times OP} + \dfrac{PR \times NP}{NP \times OP}$

$= \left(\dfrac{NQ}{ON}\right) \times \left(\dfrac{ON}{OP}\right) + \left(\dfrac{PR}{NP}\right) \times \left(\dfrac{NP}{OP}\right)$

$= \sin A \cos B + \cos A \sin B$

Now, that we have a formula for $\sin(A + B)$, deriving the formula for $\sin(A - B)$ is fairly simple:

$\sin (A - B) = \sin(A + (-B)) = \sin A \cos (-B) +\cos A \sin (-B)$

We know from , that $\cos(-B) = \cos B$ and $\sin (-B) = -\sin B$

Therefore, we get:

$\sin(A -B) = \sin A \cos B - cos A sin B$

-----------book page break-----------

II. Evaluatiing cos(A ± B):

Using the same diagram from $Fig.\ 1$, we get:

$\cos (A + B) = \dfrac{OM}{OP} = \dfrac{OQ - MQ}{OP}$

$= \dfrac{OQ}{OP} - \dfrac{MQ}{OP}$

$= \dfrac{OQ}{OP} - \dfrac{RN}{OP}$

$= \dfrac{OQ \times ON}{ON \times OP} - \dfrac{RN \times PN}{PN \times OP}$

$= \left(\dfrac{OQ}{ON}\right) \times \left(\dfrac{ON}{OP}\right) - \left(\dfrac{RN}{PN}\right) \times \left(\dfrac{PN}{OP}\right)$

$= \cos A \cos B - \sin A \sin B$

For $\cos(A - B)$, we get:

$\cos (A - B) = \cos(A + (-B)) = \cos A \cos (-B) - \sin A \sin (-B)$

$= \cos A \cos B + \sin A \sin B$

III. Evaluating tan(A ± B):

For finding out the expansion of $\tan (A \pm B)$ we will use the formula for $\sin (A \pm B)$ and $\cos (A \pm B)$ from the previous two sections.

-----------book page break-----------

$\tan (A + B) = \dfrac{\sin (A + B)}{\cos (A + B)}$

$= \dfrac{\sin A \cos B + \cos A \sin B}{\cos A \cos B - \sin A \sin B}$

$= \dfrac{\dfrac{1}{\cos A \cos B} \times \left(\sin A \cos B + \cos A \sin B\right)}{\dfrac{1}{\cos A \cos B} \times \left(\cos A \cos B - \sin A \sin B\right)}$

$= \dfrac{\dfrac{\sin A}{\cos A} + \dfrac{\sin B}{\cos B}}{1 - \dfrac{\sin A \times \sin B}{\cos A \times \cos A}}$

$= \dfrac{\tan A + \tan B}{1 - \tan A \tan B}$

(Observe, that $\because \tan A$ and $\tan B$ are finite, $A \ne 90^\circ$ and $B \ne 90^\circ$, $\therefore \cos A \ne 0$ and $\cos B \ne 0$. therefore dividing by $\cos A \cos B$ is a valid step)

Similarly,

$\tan (A - B)$

$= \dfrac{\sin (A - B)}{\cos (A - B)}$

$= \dfrac{\sin A \cos B - \cos A \sin B}{\cos A \cos B + \sin A \sin B}$

-----------book page break-----------

$= \dfrac{\dfrac{1}{\cos A \cos B} \times \left(\sin A \cos B - \cos A \sin B\right)}{\dfrac{1}{\cos A \cos B} \times \left(\cos A \cos B + \sin A \sin B\right)}$

$= \dfrac{\dfrac{\sin A}{\cos A} - \dfrac{\sin B}{\cos B}}{1 + \dfrac{\sin A \times \sin B}{\cos A \times \cos A}}$

$= \dfrac{\tan A - \tan B}{1 + \tan A \tan B}$