Problem Contributed By Community Member debroy0611
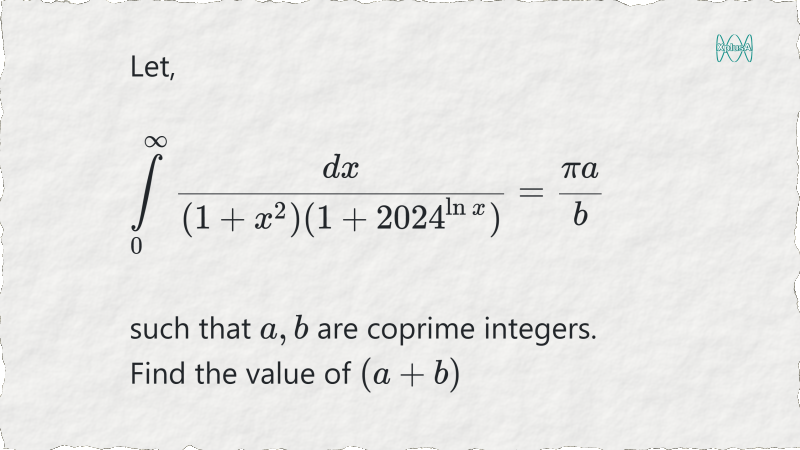
A smart integration problem from the 2024 Caltech Math Meet. This problem requires no more knowledge than basic integration.
Problem contributed by anonymous user
-----------book page break-----------
Let:
$I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{(1 + x^2)(1 + 2024^{\ln x})}$
We can write $2024$ as $e^{\ln 2024}$, which gives us:
$I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{(1 + x^2)\left(1 + \left(e^{\ln 2024}\right)^{\ln x}\right)}$
$\Rightarrow I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{(1 + x^2)\left(1 + \left(e^{\ln x}\right)^{\ln 2024}\right)}$
$\Rightarrow I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{(1 + x^2)\left(1 + x^{\ln 2024}\right)}$
Let $\ln 2024 = a$,
$\Rightarrow I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{(1 + x^2)\left(1 + x^a\right)}$ $...(i)$
-----------book page break-----------
Let $x = \dfrac{1}{u} \Rightarrow dx = -\dfrac{1}{u^2}du$
$\therefore I = \displaystyle \int \limits_\infty^{0} \dfrac{-du}{\left(1 + \left( \dfrac{1}{u} \right)^2 \right) \left(1 + \left( \dfrac{1}{u} \right)^a\right)u^2}$
$\Rightarrow I = \displaystyle \int \limits_0^{\infty} \dfrac{u^a du}{\left(u^2 + 1 \right) \left(u^a +1 \right)}$
Renaming $u$ with $x$, we get:
$I = \displaystyle \int \limits_0^{\infty} \dfrac{x^a dx}{\left(1 + x^2 \right) \left(1 + x^a \right)}$ $...(ii)$
Adding $eqns\ (i)$ and $(ii)$ we get:
$2I = \displaystyle \int \limits_0^{\infty} \dfrac{dx}{\left(1 + x^2 \right) \left(1 + x^a \right)} + \displaystyle \int \limits_0^{\infty} \dfrac{x^a dx}{\left(1 + x^2 \right) \left(1 + x^a \right)}$
$\Rightarrow 2I = \displaystyle \int \limits_0^{\infty} \dfrac{\cancel{\left(1 + x^a \right)} dx}{\left(1 + x^2 \right) \cancel{\left(1 + x^a \right)}}$
-----------book page break-----------
Substituting $x = \tan \theta$, $dx = \sec^2 \theta$ (limits $x = 0$, $\theta = 0$ and $x = \infty$, $\theta = \dfrac{\pi}{2}$), we get:
$2I = \displaystyle \int \limits_0^{\frac{\pi}{2}} \dfrac{\sec^2 \theta d \theta}{1 + \tan^2 \theta}$
$\Rightarrow 2I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \dfrac{\cancel{(\sec^2 \theta)} d \theta}{\cancel {\sec^2 \theta}} = \theta \biggr |_0^{\frac{\pi}{2}}$
$\therefore I =\dfrac{\pi}{4}$, $\Rightarrow a = 1$ and $b = 4$
$\therefore a + b = 5$