This problem from the Dutch Math Olympiad can be solved using some basic observations.

A problem from the 2017 Dutch Mathematical Olympiad that can be solved using some amount of knowledge of number theory and some smart thinking.

-----------book page break-----------

Let us start by designating each cell an identifier where the bottom-left corner cell is $C_{0,0}$ and the top-right corner cell is $C_{99, 99}$ as shown in the figure below:

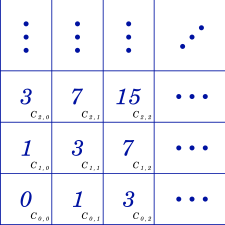
$C_{0,0}$ contains a $0$

Cell $C_{0,1}$ contains:
$(1) + (0) = 1$

Similarly, cell $C_{1,0}$ also contains $1$.

Each of cells $C_{0, 2}$, $C_{1, 1}$ and $C_{2, 0}$ will contain:

$(1 + 1) + (0 + 1) = 3$

-----------book page break-----------

Each of cells $C_{0, 3}$, $C_{1, 2}$, $C_{2, 1}$ and $C_{3, 0}$ will contain:

$(1 + 1 + 1) + (0 + 1 + 3) = 7$

For the general case $C_{m, n}$ will contain the value $2^k - 1$ for all values of $m, n$ satisfying $m + n = k$. We will see an induction based proof for the same.

Let us assume that the above assertion is true for some $k = K$.

For $k = K + 1$, the cell can be reached from $C_{0, 0}$ using $K + 1$ steps, and sum of all previous steps will be $(2^0-1) + (2^1-1) + ... + (2^K-1)$

Therefore the value in this cell will be:
$(K + 1) + \left((2^0-1) + (2^1-1) + ... + (2^K-1)\right)$

$= \cancel{(K + 1)} + \left((2^0) + (2^1) + ... + (2^K)\right) - \cancel{(K+1)}$

$= \dfrac{2^0 \left(2^{K+1}\right) - 1}{2 - 1}$

$= 2^{K+1} - 1$

For the base case, we can see that the value of cell $C_{0, 0}$ is $2^{0} -1 = 0$

For the last digit of each of this cells, we take modulo $10$ of the cell values, which give us:

$0, 1, 3, 7, 5, 1, 3, 7, 5...$

If we leave out the first term we can see that the cycle repeats at a frequency of $4$, that is $1, 3, 7, 5, 1, 3, 7, 5...$

For cell $C_{99, 99}$ the value of $K = 198$

-----------book page break-----------

$198 \% 4 = 2$ and the second term of the repeating sequence is $3$

Therefore, the $C_{99, 99}$ will contain a value ending with the digit $3$