A Community Problem Contributed By debroy0611
The very elegant integration problem from the Stanford Math Tournament will help you develop a unique way to visualize functions and their inverses when it comes to integration.
Problem contributed by anonymous user
First, let us observe the given function:
$x = f(x) e^{f(x)}$
We can see that for $x > 0$, $e^{f(x)}$ is positive, hence, $f(x)$ is also positive. Therefore, $f(x)$ increases monotonically with $x$.
-----------book page break-----------
Let $y = f(x)$, therefore, we get:
$x = y e^y$
If we consider $y e^y = g(y)$, then $g(y) = x$ and $g$ is the inverse function of $f$
Now, let us make some observations regarding the function.
For $y = 0$, $x = 0$, and for $y = 1$, $x = e$
Now let us plot the approximate graph of $y = f(x)$
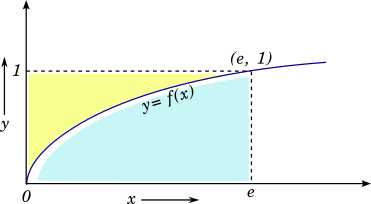
The area shown in blue shows us the value of the integral we are looking for.
This value can be obtained by subtracting the yellow region from the rectangle.
-----------book page break-----------
Therefore,
$\displaystyle \int\limits_0^e f(x) dx$
$= [\text{area of the rectangle}] - [\text{area of yellow region}]$
$= e \times 1 - \displaystyle \int\limits_0^1 f^{-1}(y) dy$
$= e - \displaystyle \int\limits_0^1 g(y)dy$
$= e - \displaystyle \int\limits_0^1 y e^y dy$
Let us first evaluate:
$\displaystyle \int\limits_0^1 ye^ydy$
We can evaluate the integral using integration by parts, but in this case will use simple observation to solve this.
$\dfrac{d}{dy} y e^y = ye^y + e^y$
-----------book page break-----------
Therefore,
$\dfrac{d}{dy} (y e^y - e^y) = ye^y + e^y -e^y = ye^y$
$\Rightarrow \displaystyle \int ye^ydy = y e^y - e^y$
Taking the limits:
$\displaystyle \int\limits_0^1 ye^ydy = (y e^y - e^y) {\Biggr|}_0^1$
$\Rightarrow \displaystyle \int\limits_0^1 ye^ydy = (1 \cdot e^1 - e^1) - (0 \cdot e^0 - e^0)$
$\Rightarrow \displaystyle \int\limits_0^1 ye^ydy = (e^1 - e^1) - (0 - 1) = 1$
Therefore, the area of the blue region, which gives us our integral is,:
$e - 1$