How Do You Solve This Problem Without Knowing The Dimensions Of The Rectangle?
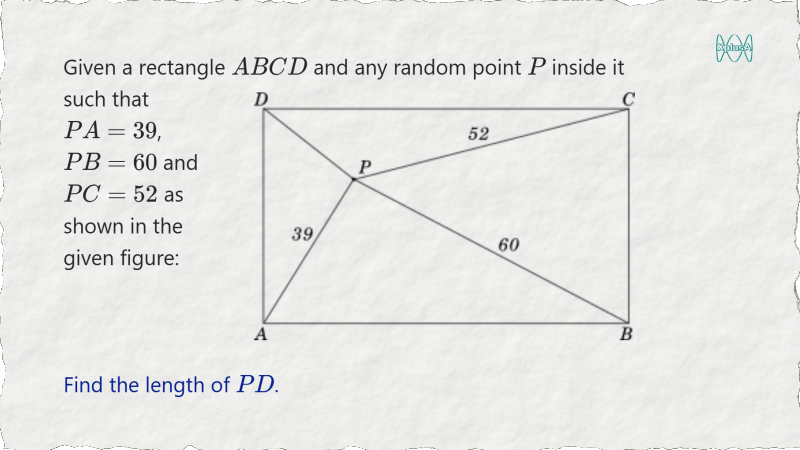
This seemingly easy and yet elegant problem shows you how to find a solution without knowing some obvious information about the problem.
-----------book page break-----------
Let us draw the line $RS$ through $P$ such that $RS || AD$ as shown in the figure below:
Let $|PD| = x$, $|PS| = l$ and $|PR| = k$
Since $PS \parallel AD \parallel BC$
$DS = AR = m\ (let)$
and
$CS = BR = n\ (let)$
Considering right angled $\triangle PSD$,
$l^2 + m^2 = x^2$ $...(i)$
-----------book page break-----------
Similarly, from $\triangle PSC$,
$l^2 + n^2 = 52^2$ $...(ii)$
From $\triangle PRA$,
$k^2 + m^2 = 39^2$ $...(iii)$
From $\triangle PRB$
$k^2 + n^2 = 60^2$ $...(iv)$
Adding equations $(i)$ and $(iv)$, we get:
$k^2 + l^2 + m^2 + n^2 = x^2 + 60^2$ $...(v)$
Similarly, adding equations $(ii)$ and $(iii)$, we get:
$k^2 + l^2 + m^2 + n^2 = 52^2 + 39^2$ $...(vi)$
Combining equations $(v)$ and $(vi)$, we get:
$x^2 + 60^2 = 52^2 + 39^2$
$\Rightarrow x^2 = 52^2 + 39^2 - 60^2$
$\Rightarrow x^2 = 2704 + 1521 - 3600 = 625$
$\Rightarrow x = 25$