A Community Problem Contributed By Our Member debroy0611
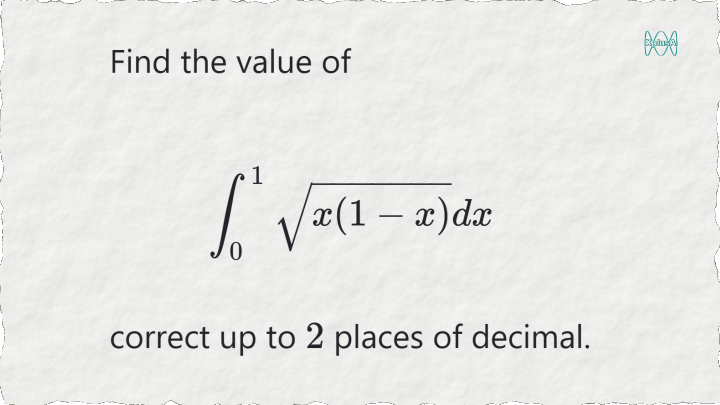
The easiest problem you have ever seen, if you catch the trick, a very difficult one otherwise.
Problem contributed by anonymous user
We will solve this problem using a simple geometric approach, instead of attempting a calculus based approach:
Let:
$y = \sqrt{x(1-x)}$
$\Rightarrow y^2 = x - x^2$
$\Rightarrow x^2 - x + y^2 = 0$
-----------book page break-----------
$\Rightarrow x^2 - 2 \cdot \dfrac{1}{2} \cdot x + \dfrac{1}{4} + y^2 = \dfrac{1}{4}$
$\Rightarrow \left(x - \dfrac{1}{2} \right)^2 + (y - 0)^2 = \left(\dfrac{1}{2}\right)^2$
The above is the equation of a circle with radius $\dfrac{1}{2}$, and centered at $\left( \dfrac{1}{2}, 0 \right)$

Since the problem is asking for the integral of $\sqrt{x(1-x)}$, this is given by the positive half of the circle.
Therefore, the area is:
$\dfrac{1}{2} \pi \left( \dfrac{1}{2} \right)^2$
$= \dfrac{\pi}{8} \approx 0.39$