A Very Simple Problem That Just Requires Some Imagination

This problem requires no more than some fundamental concept of geometry and your ability to imagine geometric shape.
-----------book page break-----------
The shortest path to the jelly drop is not along any of the edges of the box.
Imagine opening the box as shown below, such that the top surface is in the same plane as the front surface.
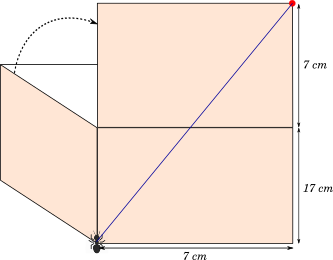
Then the shortest path of the ant will be a straight line along this surface.
Therefore the shortest path will be:
$\sqrt{7^2 + (17 + 7)^2}\ cm$
-----------book page break-----------
$= \sqrt{7^2 + 24^2}\ cm$
$= \sqrt{49 + 576}\ cm$
$= \sqrt{625}\ cm$
$= 25\ cm$
Once you have drawn the shortest straight line along the surface, the distance along the line will remain same even with the lid closed.