The Magic Of Construction. Try It Now.
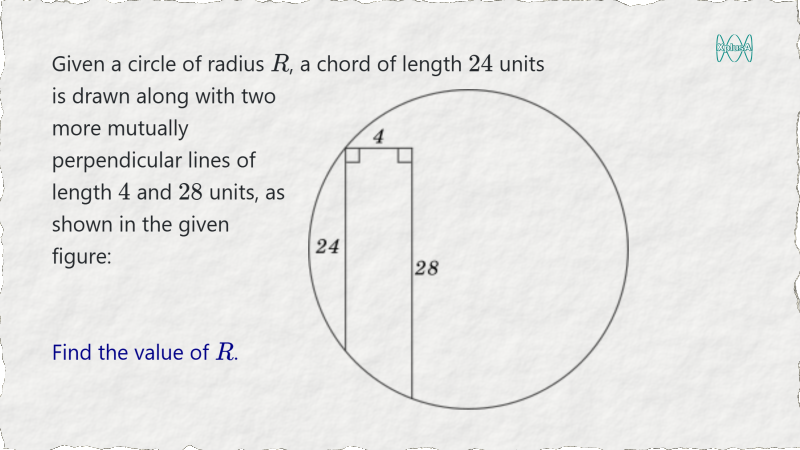
This seemingly confusing problem can be solved easily using a few smart constructions.
-----------book page break-----------
Let us draw the following.
Complete the larger chord $CD$. From the center $O$, draw perpendicular $OP$ to the smaller chord $AB$.
Join the two radii $OB$ and $OD$ as shown in the figure below.
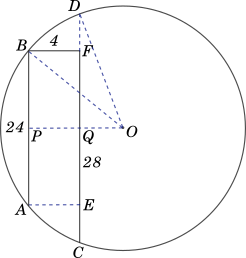
Since $AB \parallel CD$, the line $OP \perp AB$, it is also perpendicular to $CD$.
$ABFE$ is a rectangle, therefore $FE = 24$
-----------book page break-----------
$OP$ bisects both $AB$ and $EF$.
$\therefore QE = QF = 24 \div 2 = 12$
Also,
$FD = EC = EF - AB = 28 - 24 = 4$
We also have:
$QD = QF + FD = 12 + 4 = 16$
and
$OP = OQ + 4$
Using right angled $\triangle OQD$, we have
$OD^2 = OQ^2 + QD^2$
$\Rightarrow r^2 = OQ^2 + 16^2$ $...(i)$
Similarly, using right angled $\triangle OPB$
$OB^2 = OP^2 + PB^2$
$\Rightarrow r^2 = (OQ+4)^2 + 12^2$ $...(ii)$
Combining $(ii)$ and $(i)$
$OQ^2 + 16^2 = (OQ+4)^2 + 12^2$
$\Rightarrow OQ^2 + 16^2 = OQ^2 + 8 OQ + 4^2 + 12^2$
$\Rightarrow 8OQ = 16^2 - 12^2 - 4^2$
$\Rightarrow OQ = 12$
Substituting the value of $OQ$ in equation $(i)$ we get:
$r^2 = 12^2 + 16^2$
$r^2 = 4^2 (3^2 + 4^2)$
$r = \sqrt{4^2 \times 25} = 4 \times 5 = 20$