A Neat Way To Solve An Alternating Harmonic Series
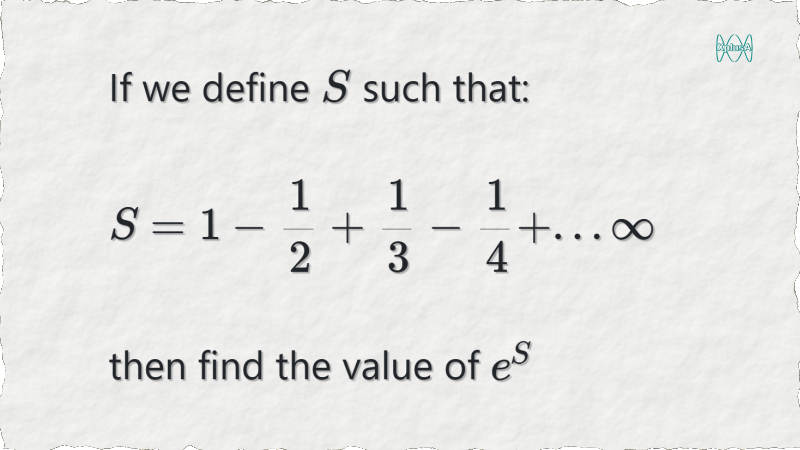
Here is an alternating harmonic series that converges. Do you know how to find the sum?
Let us re-define the given series as a function of $x$:
$f(x) = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \dfrac{x^4}{4} + ... \infty $ where $x \in (-1, 1)$
Once we have evaluated this series for some general $x$, we can find $f(1)$ to get the answer to our problem.
Differentiating our function, we get:
$f'(x) = 1 - \dfrac{2x}{2} + \dfrac{3x^2}{3} - \dfrac{4x^3}{4} + ... \infty $
-----------book page break-----------
$\Rightarrow f'(x) = 1 - x + x^2 - x^3 + ... \infty $
Since we have taken $x \in (-1, 1)$, we can consider this above function as a converging geometric series with $-x$ as the common ratio.
Therefore, we get:
$\Rightarrow f'(x) = \dfrac{1}{1 - (-x)} = \dfrac{1}{1 + x}$
Now, $f'(x)$ is divergent for $x > 1$ and for $x = 1$, it is undefined.
Therefore, instead of doing a direct integration, we will integrate $f'(x)$ from $0$ to $1 - \delta$, where $\delta$ is positive and take the limit $\delta \rightarrow 0$
Therefore,
$\displaystyle \int \limits_{0}^{1-\delta} f'(x) dx = \int \limits_{0}^{1-\delta} \dfrac{1}{1 + x} dx$
$\Rightarrow f(x) {\Biggr |}_0^{1-\delta} = (\ln |1 + x|) {\Biggr |}_0^{1-\delta}$
$f(0) = 0$ and $\ln|1 + 0| = 0$, therefore we get the above integral as:
$f(1 - \delta) = \ln |1 + (1 - \delta)|$
Now taking the limit $\delta \rightarrow 0$ we get:
$\lim \limits_{\delta \rightarrow 0} f(1 - \delta) = \lim \limits_{\delta \rightarrow 0} \ln |1 + (1 - \delta)|$
$\Rightarrow f(1) = \ln (1 + 1) = \ln 2$
-----------book page break-----------
Therefore,
$1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4}... \infty = \ln 2$
Therefore, $S = \ln 2 \Rightarrow e ^ S = e^{\ln 2} = 2$