A Relatively Easy Problem From Putnam 2005
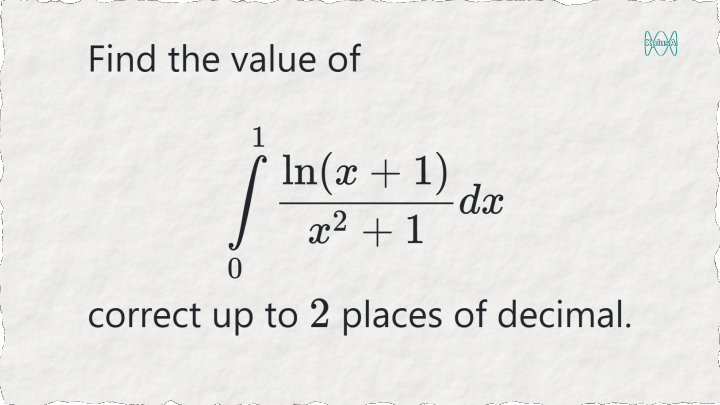
This one is a fairly easy one from the arsenal of Putnam. This one appeared in 2005.
Problem contributed by anonymous user
Let:
$I = \displaystyle \int \limits_0^1 \dfrac{\ln (x + 1)}{x^2 + 1} dx$
As a first step let us substitute $x = \tan u$, which gives us:
$dx = \sec^2 u du$ and the limits will be from $u = 0$ to $u = \dfrac{\pi}{4}$
-----------book page break-----------
Therefore,
$I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \dfrac{\ln (\tan u + 1)}{\tan^2 u + 1} \sec^2 u du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \dfrac{\ln (\tan u + 1)}{\cancel {\sec^2 u}} \cancel{\sec^2 u} du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln (\tan u + 1) du$
Applying King's Rule, we get:
$I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\tan \left(\dfrac{\pi}{4} - u \right) + 1 \right) du$
Expanding $\tan \left(\dfrac{\pi}{4} - u \right)$, using the formula described we get:
$I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\dfrac{\tan \left(\dfrac{\pi}{4}\right) - \tan u}{1 + \tan \left(\dfrac{\pi}{4}\right) \tan u} + 1 \right) du$
-----------book page break-----------
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\dfrac{1 - \tan u}{1 + \tan u} + 1 \right) du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\dfrac{1 - \tan u}{1 + \tan u} + 1 \right) du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\dfrac{1 - \cancel{\tan u} + 1 + \cancel{\tan u}}{1 + \tan u}\right) du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln \left(\dfrac{2}{1 + \tan u}\right) du$
$\Rightarrow I = \displaystyle \int \limits_0^{\frac{\pi}{4}} \ln 2 - \ln \left( 1 + \tan u \right) du$
$\Rightarrow I = \displaystyle \ln 2 \int \limits_0^{\frac{\pi}{4}} du - \int \limits_0^{\frac{\pi}{4}} \ln \left( 1 + \tan u \right) du$
-----------book page break-----------
$\Rightarrow I = \displaystyle \ln 2 \int \limits_0^{\frac{\pi}{4}} du - I$
$\Rightarrow 2I = \dfrac{\pi}{4} \ln 2$
$\therefore I = \dfrac{\pi}{8} \ln 2 \approx 0.27$