A Simple Problem Involving Inverse Functions
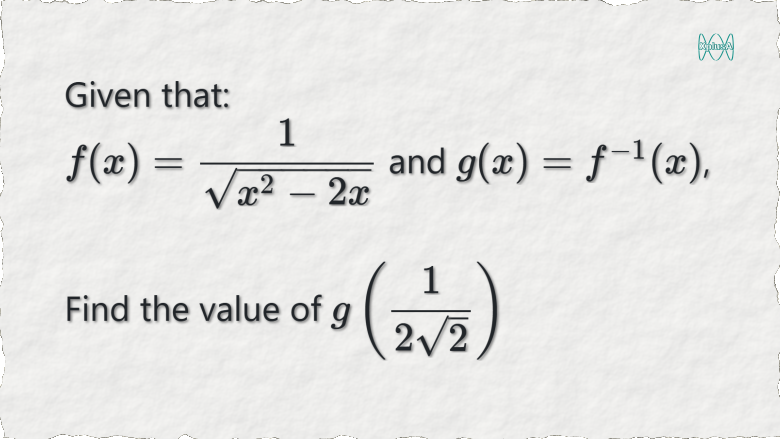
Here is a simple problem involving function inverses, designed to develop your thinking process with handling of functions.
Since $g(x) = f^{-1}(x)$,
$g(f(x)) = x$
$\Rightarrow g\left( \dfrac{1}{\sqrt{x^2 - 2x}} \right) = x$
-----------book page break-----------
Let $ \dfrac{1}{\sqrt{x^2 - 2x}} = t$
$\Rightarrow \dfrac{1}{x^2 - 2x} = t^2$
$\Rightarrow x^2 - 2x = \dfrac{1}{t^2}$
$\Rightarrow x^2 - 2x + 1= \dfrac{1}{t^2} + 1$
$\Rightarrow (x - 1)^2 = \left(\sqrt{\dfrac{1}{t^2} + 1} \right)^2$
$\Rightarrow x - 1 = \sqrt{\dfrac{1}{t^2} + 1}$
$\Rightarrow x = 1 + \sqrt{\dfrac{1}{t^2} + 1}$
Therefore,
$g(t) = x = 1 + \sqrt{\dfrac{1}{t^2} + 1}$
-----------book page break-----------
Therefore,
$g\left( \dfrac{1}{2 \sqrt{2}} \right)$
$= 1 + \sqrt{(2\sqrt{2})^2 + 1}$
$= 1 + \sqrt{9}$
$= 4$