A Problem From Singapore Junior Math Olympiad
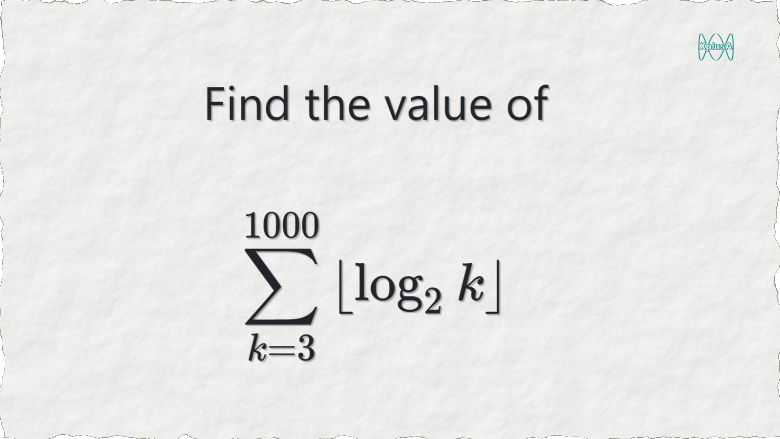
Here is an easy one from the Singapore Junior Math Olympiad.
For any value $a$ such that $2^k \le n \lt 2^{k+1}$, where $k$ is an integer,
$\log_{2} a = k + x$, where $0 \le x \lt 1$
$\therefore \left\lfloor \log_{2} a \right\rfloor = k$
For example,
$\left\lfloor \log_{2} 2 \right\rfloor = 1$, $\left\lfloor \log_{2} 3 \right\rfloor = 1$
-----------book page break-----------
$\left\lfloor \log_{2} 4 \right\rfloor = 2$, $\left\lfloor \log_{2} 5 \right\rfloor = 2$, $\left\lfloor \log_{2} 6 \right\rfloor = 2$, $\left\lfloor \log_{2} 7 \right\rfloor = 2$
The number of integer values $n$ satisfying,
$2^k \le n \lt 2^{k+1}$ is $2^{k+1} - 2^k = 2^k(2 - 1) = 2^k$
We can split the given sum to make the range between two perfect powers of $2$, which gives us:
$\displaystyle \sum\limits_{k = 3}^{1000}\left\lfloor \log_{2}k\right\rfloor$
$= \displaystyle \left\lfloor \log_{2}3\right\rfloor + \sum\limits_{k = 4}^{1023}\left\lfloor \log_{2}k\right\rfloor - \sum\limits_{k = 1001}^{1023}\left\lfloor \log_{2}k\right\rfloor$
$= \displaystyle \left\lfloor \log_{2}3\right\rfloor + \sum \limits_{i = 2}^{9} \sum\limits_{k = 2^i}^{2^{i+1}-1}\left\lfloor \log_{2}k\right\rfloor - \sum\limits_{k = 1001}^{1023}\left\lfloor \log_{2}k\right\rfloor$
$= 1 + \left( 4 \times 2 + 8 \times 3 + ... 512 \times 9 \right) - 23 \times 9$
Let us find the sum of the middle portion using $AP$, $GP$ technique:
Let:
$S = 4 \times 2 + 8 \times 3 + ... 512 \times 9 $
$2S = \phantom{0000000} 8 \times 2 + 16 \times 3 + ... + 512 \times 8 + 1024\times 9$
$S = -4 \times 2 + 8 \times (2 - 3) + 16 \times (3 - 4) ... 512 \times (8 - 9) + 1024 \times 9$
-----------book page break-----------
$= -8 - (8 + 16 + ... 512) + 1024 \times 9$
$= -8 - \dfrac{8 (2^7 - 1)}{2 - 1} + 1024 \times 9$
$= -2^{10} + 2^{10} \times 9$
$= 2 ^ {10} \times 2^3 = 2 ^ {13} = 8192$
Therefore,
$\displaystyle \sum\limits_{k = 3}^{1000}\left\lfloor \log_{2}k\right\rfloor$
$= 1 + 8192 - 23 \times 9$
$= 8193 - 207$
$= 7986$