A Community Problem Contributed By Member debroy0611

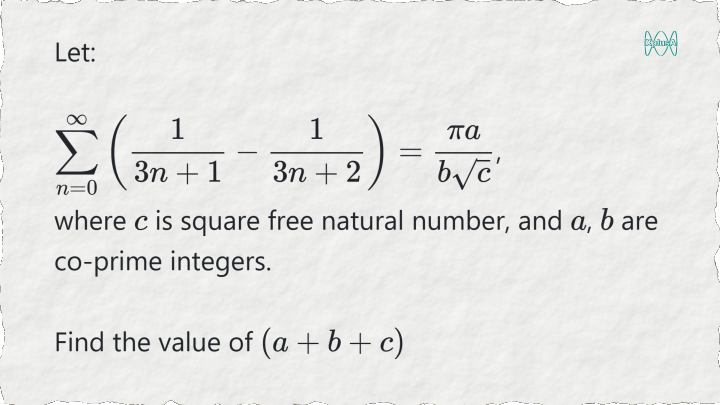
image containing math problem statement
A problem that requires more out of the box thinking than blind application theory.
Problem contributed by debroy0611
-----------book page break-----------
This is not a directly summable problem. To find the sum we will first convert each term terms to an integral problem.
$\dfrac{1}{3n+1} - \dfrac{1}{3n+2}$

We know that $\displaystyle \int x^n = \dfrac{x^{n+1}}{n+1}$

Therefore, we can write:
 $\dfrac{1}{3n+1} = \displaystyle \int \limits_{0}^{1} x^{3n} dx$
and
$\dfrac{1}{3n+2} = \displaystyle \int \limits_{0}^{1} x^{3n+1} dx$

Therefore, we can write our original summation problem as:

$\displaystyle \sum \limits_{n=0}^\infty \left( \dfrac{1}{3n+1} - \dfrac{1}{3n+2}\right)$

$= \displaystyle \sum \limits_{n=0}^\infty \left( \int \limits_{0}^{1} x^{3n} dx - \int \limits_{0}^{1} x^{3n+1} dx \right)$

-----------book page break-----------
$= \displaystyle \sum \limits_{n=0}^\infty \int \limits_{0}^{1} \left( x^{3n} -  x^{3n+1} \right) dx$

$= \displaystyle  \int \limits_{0}^{1} \left( \sum \limits_{n=0}^\infty x^{3n} - \sum \limits_{n=0}^\infty x^{3n+1} \right) dx$

$= \displaystyle \int \limits_{0}^{1} \left( \sum \limits_{n=0}^\infty x^{3n} - x \sum \limits_{n=0}^\infty x^{3n} \right) dx$

$= \displaystyle \int \limits_{0}^{1} \left( (1-x) \sum \limits_{n=0}^\infty x^{3n}\right) dx$

We can see that $\sum \limits_{n=0}^\infty x^{3n}$ is a geometric series with $1$ as the first term and $x^3$ as the common ratio.
Therefore,
$\sum \limits_{n=0}^\infty x^{3n} = \dfrac{1}{1 - x^3}$

Therefore our integral becomes:
$= \displaystyle \int \limits_{0}^{1} \left( (1-x) \times \dfrac{1}{1 - x^3} \right) dx$

-----------book page break-----------
$= \displaystyle \int \limits_{0}^{1} \left( \cancel{(1-x)} \times \dfrac{1}{ \cancel{(1-x)}  (1 + x + x^2)} \right) dx$

$= \displaystyle \int \limits_{0}^{1} \left( \cancel{(1-x)} \times \dfrac{1}{ \cancel{(1-x)}  \left(\dfrac{1}{4} + 2\cdot\dfrac{1}{2}\cdot x + x^2 \right) + \dfrac{3}{4}} \right) dx$

$= \displaystyle \int \limits_{0}^{1} \dfrac{1}{\left(x + \dfrac{1}{2} \right)^2 + \left( \dfrac{\sqrt{3}}{2} \right)^2} dx$

$= \left[ \dfrac{2}{\sqrt{3}} \tan^{-1} \left(\dfrac{2}{\sqrt{3}} \left(x + \dfrac{1}{2} \right) \right) \right]_0^1$

$= \dfrac{2}{\sqrt{3}} \left( \tan^{-1} \sqrt{3} - \tan^{-1} \dfrac{1}{\sqrt{3}} \right)$

$= \dfrac{2}{\sqrt{3}} \left( \dfrac{2 \pi}{3} - \dfrac{\pi }{3} \right) $

$= \dfrac{2 \pi}{3 \sqrt{3}}$

-----------book page break-----------
Therefore
$\dfrac{2 \pi}{3 \sqrt{3}} = \dfrac{\pi a}{b \sqrt{c}}$

$\Rightarrow a = 2, b = 3, c = 3$

$\therefore (a + b + c) = 8$