A Member Contribution Picked From The Stanford Math Tournament
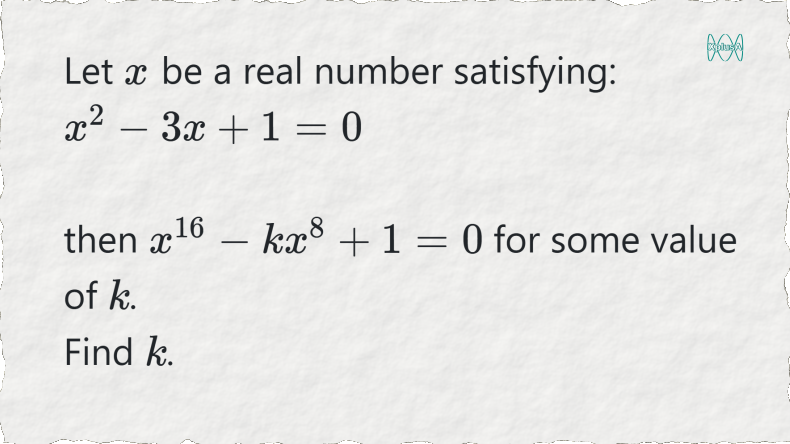
This problem was used as a tie-breaker problem at the Stanford Math Tournament. This is a relatively simple problem, requiring no more than some smart handling of the problem.
Problem contributed by anonymous user
Using the given equation, we get:
$x^2 - 3x + 1 = 0$
$\Rightarrow x - 3 + \dfrac{1}{x} = 0$
$\Rightarrow x + \dfrac{1}{x} = 3$
-----------book page break-----------
$\Rightarrow \left( x + \dfrac{1}{x} \right)^2 = 3^2$
$\Rightarrow x^2 + \dfrac{1}{x^2} = 9 - 2 = 7$
$\Rightarrow \left( x^2 + \dfrac{1}{x^2} \right)^2 = 49$
$\Rightarrow x^4 + \dfrac{1}{x^4} = 47$
$\Rightarrow \left( x^4 + \dfrac{1}{x^4} \right)^2 = 2209$
$\Rightarrow x^8 + \dfrac{1}{x^8} = 2207$
$\Rightarrow x^{16} + 1 = 2207x^8$
$\Rightarrow x^{16} - 2207x^8 + 1 = 0$
Therefore, $k = 2207$