A Series Problem Based On Trigonometric Function.

$\newcommand{\xacomb}[2]{\raise{0.5em}{\small{#1}} C_{#2}}$ $\newcommand{\xaperm}[2]{\raise{0.5em}{\small{#1}} P_{#2}}$ $\newcommand{\xasuper}[1]{\raise{0.4em}{\underline{#1}}}$ $\newcommand{\xatooltipc}[2]{\xatooltip{\color{green}{#1}}{#2}}$ $\newcommand{\xatooltipcc}[3]{\xatooltip{\color{#1}{#2}}{#3}}$ $\newcommand{\xafactorial}[1]{\bbox[border-left: 1px solid black; border-bottom: 2px solid black; padding-left: 2px; padding-bottom: 2px; padding-right: 3px; padding-top: 2px;]{#1}}$ $\DeclareMathOperator{\sech}{sech}$ $\DeclareMathOperator{\csch}{csch}$ $\newcommand{\placeholder}[1]{}$ $\newcommand{\strut}[0]{\phantom{\rule[0.3\baselineskip]{0}{0.7\baselineskip}}}$ $\newcommand{\iff}[0]{\;\Longleftrightarrow\;}$ $\newcommand{\nicefrac}[2]{^{#1}\!\!/\!_{#2}}$ $\newcommand{\phase}[1]{\enclose{phasorangle}{#1}}$ $\newcommand{\rd}[0]{\mathrm{d}}$ $\newcommand{\rD}[0]{\mathrm{D}}$ $\newcommand{\odif}[0]{\mathrm{d}}$ $\newcommand{\doubleStruckCapitalN}[0]{\mathbb{N}}$ $\newcommand{\doubleStruckCapitalR}[0]{\mathbb{R}}$ $\newcommand{\doubleStruckCapitalQ}[0]{\mathbb{Q}}$ $\newcommand{\doubleStruckCapitalZ}[0]{\mathbb{Z}}$ $\newcommand{\doubleStruckCapitalP}[0]{\mathbb{P}}$ $\newcommand{\scriptCapitalE}[0]{\mathscr{E}}$ $\newcommand{\scriptCapitalH}[0]{\mathscr{H}}$ $\newcommand{\scriptCapitalL}[0]{\mathscr{L}}$ $\newcommand{\gothicCapitalC}[0]{\mathfrak{C}}$ $\newcommand{\gothicCapitalH}[0]{\mathfrak{H}}$ $\newcommand{\gothicCapitalI}[0]{\mathfrak{I}}$ $\newcommand{\gothicCapitalR}[0]{\mathfrak{R}}$ $\newcommand{\imaginaryI}[0]{\mathrm{i}}$ $\newcommand{\imaginaryJ}[0]{\mathrm{j}}$ $\newcommand{\exponentialE}[0]{\mathrm{e}}$ $\newcommand{\differentialD}[0]{\mathrm{d}}$ $\newcommand{\capitalDifferentialD}[0]{\mathrm{D}}$ $\newcommand{\mathstrut}[0]{\vphantom{(}}$ $\newcommand{\angl}[1]{\enclose{actuarial}{#1}}$ $\newcommand{\angln}[0]{\enclose{actuarial}{n}}$ $\newcommand{\anglr}[0]{\enclose{actuarial}{r}}$ $\newcommand{\anglk}[0]{\enclose{actuarial}{k}}$ $\newcommand{\ordinarycolon}[0]{:}$ $\newcommand{\vcentcolon}[0]{\mathrel{\mathop\ordinarycolon}}$ $\newcommand{\dblcolon}[0]{{\mathop{\unicode{0x2237}}}}$ $\newcommand{\coloneqq}[0]{{\mathop{\unicode{0x2254}}}}$ $\newcommand{\Coloneqq}[0]{{\mathop{\unicode{0x2A74}}}}$ $\newcommand{\coloneq}[0]{{\mathop{\unicode{0x2254}}}}$ $\newcommand{\Coloneq}[0]{{\mathop{\unicode{0x2A74}}}}$ $\newcommand{\eqqcolon}[0]{{\mathop{\unicode{0x2255}}}}$ $\newcommand{\Eqqcolon}[0]{{\mathop{\unicode{0x3D}\unicode{0x2237}}}}$ $\newcommand{\eqcolon}[0]{{\mathop{unicode{0x2255}}}}$ $\newcommand{\Eqcolon}[0]{{\mathop{\unicode{0x3D}\unicode{0x2237}}}}$ $\newcommand{\colonapprox}[0]{{\mathop{\unicode{0x003A}\unicode{0x2248}}}}$ $\newcommand{\Colonapprox}[0]{{\mathop{\unicode{0x2237}\unicode{0x2248}}}}$ $\newcommand{\colonsim}[0]{{\mathop{\unicode{0x3A}\unicode{0x223C}}}}$ $\newcommand{\Colonsim}[0]{{\mathop{\unicode{0x2237}\unicode{0x223C}}}}$ $\newcommand{\colondash}[0]{\mathrel{\vcentcolon\mathrel{\mkern-1.2mu}\mathrel{-}}}$ $\newcommand{\Colondash}[0]{\mathrel{\dblcolon\mathrel{\mkern-1.2mu}\mathrel{-}}}$ $\newcommand{\dashcolon}[0]{\mathrel{\mathrel{-}\mathrel{\mkern-1.2mu}\vcentcolon}}$ $\newcommand{\Dashcolon}[0]{\mathrel{\mathrel{-}\mathrel{\mkern-1.2mu}\dblcolon}}$ $\newcommand{\ratio}[0]{\vcentcolon}$ $\newcommand{\coloncolon}[0]{\dblcolon}$ $\newcommand{\colonequals}[0]{\coloneq}$ $\newcommand{\coloncolonequals}[0]{\Coloneq}$ $\newcommand{\equalscolon}[0]{\eqcolon}$ $\newcommand{\equalscoloncolon}[0]{\Eqcolon}$ $\newcommand{\colonminus}[0]{\colondash}$ $\newcommand{\coloncolonminus}[0]{\Colondash}$ $\newcommand{\minuscolon}[0]{\dashcolon}$ $\newcommand{\minuscoloncolon}[0]{\Dashcolon}$ $\newcommand{\coloncolonapprox}[0]{\Colonapprox}$ $\newcommand{\coloncolonsim}[0]{\Colonsim}$ $\newcommand{\simcolon}[0]{\mathrel{\sim\mathrel{\mkern-1.2mu}\vcentcolon}}$ $\newcommand{\Simcolon}[0]{\mathrel{\sim\mathrel{\mkern-1.2mu}\dblcolon}}$ $\newcommand{\simcoloncolon}[0]{\mathrel{\sim\mathrel{\mkern-1.2mu}\dblcolon}}$ $\newcommand{\approxcolon}[0]{\mathrel{\approx\mathrel{\mkern-1.2mu}\vcentcolon}}$ $\newcommand{\Approxcolon}[0]{\mathrel{\approx\mathrel{\mkern-1.2mu}\dblcolon}}$ $\newcommand{\approxcoloncolon}[0]{\mathrel{\approx\mathrel{\mkern-1.2mu}\dblcolon}}$ $\newcommand{\notni}[0]{\mathrel{\unicode{0x220C}}}$ $\newcommand{\limsup}[0]{\operatorname*{lim\,sup}}$ $\newcommand{\liminf}[0]{\operatorname*{lim\,inf}}$ $\newcommand{\injlim}[0]{\operatorname*{inj\,lim}}$ $\newcommand{\projlim}[0]{\operatorname*{proj\,lim}}$ $\newcommand{\varlimsup}[0]{\operatorname*{\overline{lim}}}$ $\newcommand{\varliminf}[0]{\operatorname*{\underline{lim}}}$ $\newcommand{\varinjlim}[0]{\operatorname*{\underrightarrow{lim}}}$ $\newcommand{\varprojlim}[0]{\operatorname*{\underleftarrow{lim}}}$ $\newcommand{\argmin}[0]{\operatorname*{arg\,min}}$ $\newcommand{\argmax}[0]{\operatorname*{arg\,max}}$ $\newcommand{\plim}[0]{\mathop{\operatorname{plim}}\limits}$ $\newcommand{\tripledash}[0]{\vphantom{-}\raise{4mu}{\mkern1.5mu\rule{2mu}{1.5mu}\mkern{2.25mu}\rule{2mu}{1.5mu}\mkern{2.25mu}\rule{2mu}{1.5mu}\mkern{2mu}}}$ $\newcommand{\bra}[1]{\mathinner{\langle{#1}|}}$ $\newcommand{\ket}[1]{\mathinner{|{#1}\rangle}}$ $\newcommand{\braket}[1]{\mathinner{\langle{#1}\rangle}}$ $\newcommand{\set}[1]{\mathinner{\lbrace #1 \rbrace}}$ $\newcommand{\Bra}[1]{\left\langle #1\right|}$ $\newcommand{\Ket}[1]{\left|#1\right\rangle}$ $\newcommand{\Braket}[1]{\left\langle{#1}\right\rangle}$ $\newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace}$ $\newcommand{\varGamma}[0]{\mathit{\Gamma}}$ $\newcommand{\varDelta}[0]{\mathit{\Delta}}$ $\newcommand{\varTheta}[0]{\mathit{\Theta}}$ $\newcommand{\varLambda}[0]{\mathit{\Lambda}}$ $\newcommand{\varXi}[0]{\mathit{\Xi}}$ $\newcommand{\varPi}[0]{\mathit{\Pi}}$ $\newcommand{\varSigma}[0]{\mathit{\Sigma}}$ $\newcommand{\varUpsilon}[0]{\mathit{\Upsilon}}$ $\newcommand{\varPhi}[0]{\mathit{\Phi}}$ $\newcommand{\varPsi}[0]{\mathit{\Psi}}$ $\newcommand{\varOmega}[0]{\mathit{\Omega}}$ $\newcommand{\pmod}[1]{\quad(\operatorname{mod}\ #1)}$ $\newcommand{\mod}[1]{\quad\operatorname{mod}\,\,#1}$ $\newcommand{\bmod}[0]{\;\mathbin{\operatorname{mod }}}$ $\newcommand{\darr}[0]{\downarrow}$ $\newcommand{\dArr}[0]{\Downarrow}$ $\newcommand{\Darr}[0]{\Downarrow}$ $\newcommand{\lang}[0]{\langle}$ $\newcommand{\rang}[0]{\rangle}$ $\newcommand{\uarr}[0]{\uparrow}$ $\newcommand{\uArr}[0]{\Uparrow}$ $\newcommand{\Uarr}[0]{\Uparrow}$ $\newcommand{\C}[0]{\mathbb{C}}$ $\newcommand{\H}[0]{\mathbb{H}}$ $\newcommand{\N}[0]{\mathbb{N}}$ $\newcommand{\Q}[0]{\mathbb{Q}}$ $\newcommand{\R}[0]{\mathbb{R}}$ $\newcommand{\Z}[0]{\mathbb{Z}}$ $\newcommand{\alef}[0]{\aleph}$ $\newcommand{\alefsym}[0]{\aleph}$ $\newcommand{\Alpha}[0]{\mathrm{A}}$ $\newcommand{\Beta}[0]{\mathrm{B}}$ $\newcommand{\bull}[0]{\bullet}$ $\newcommand{\Chi}[0]{\mathrm{X}}$ $\newcommand{\clubs}[0]{\clubsuit}$ $\newcommand{\cnums}[0]{\mathbb{C}}$ $\newcommand{\Complex}[0]{\mathbb{C}}$ $\newcommand{\Dagger}[0]{\ddagger}$ $\newcommand{\diamonds}[0]{\diamondsuit}$ $\newcommand{\doublecap}[0]{\Cap}$ $\newcommand{\doublecup}[0]{\Cup}$ $\newcommand{\empty}[0]{\emptyset}$ $\newcommand{\Epsilon}[0]{\mathrm{E}}$ $\newcommand{\Eta}[0]{\mathrm{H}}$ $\newcommand{\exist}[0]{\exists}$ $\newcommand{\hArr}[0]{\Leftrightarrow}$ $\newcommand{\harr}[0]{\leftrightarrow}$ $\newcommand{\Harr}[0]{\Leftrightarrow}$ $\newcommand{\hearts}[0]{\heartsuit}$ $\newcommand{\image}[0]{\Im}$ $\newcommand{\infin}[0]{\infty}$ $\newcommand{\Iota}[0]{\mathrm{I}}$ $\newcommand{\isin}[0]{\in}$ $\newcommand{\Kappa}[0]{\mathrm{K}}$ $\newcommand{\larr}[0]{\leftarrow}$ $\newcommand{\Larr}[0]{\Leftarrow}$ $\newcommand{\lArr}[0]{\Leftarrow}$ $\newcommand{\lrarr}[0]{\leftrightarrow}$ $\newcommand{\Lrarr}[0]{\Leftrightarrow}$ $\newcommand{\lrArr}[0]{\Leftrightarrow}$ $\newcommand{\Mu}[0]{\mathrm{M}}$ $\newcommand{\natnums}[0]{\mathbb{N}}$ $\newcommand{\Nu}[0]{\mathrm{N}}$ $\newcommand{\Omicron}[0]{\mathrm{O}}$ $\newcommand{\part}[0]{\partial}$ $\newcommand{\plusmn}[0]{\pm}$ $\newcommand{\rarr}[0]{\rightarrow}$ $\newcommand{\Rarr}[0]{\Rightarrow}$ $\newcommand{\rArr}[0]{\Rightarrow}$ $\newcommand{\real}[0]{\Re}$ $\newcommand{\reals}[0]{\mathbb{R}}$ $\newcommand{\Reals}[0]{\mathbb{R}}$ $\newcommand{\restriction}[0]{\upharpoonright}$ $\newcommand{\Rho}[0]{\mathrm{P}}$ $\newcommand{\sdot}[0]{\cdot}$ $\newcommand{\sect}[0]{\S}$ $\newcommand{\spades}[0]{\spadesuit}$ $\newcommand{\sub}[0]{\subset}$ $\newcommand{\sube}[0]{\subseteq}$ $\newcommand{\supe}[0]{\supseteq}$ $\newcommand{\Tau}[0]{\mathrm{T}}$ $\newcommand{\thetasym}[0]{\vartheta}$ $\newcommand{\varcoppa}[0]{\coppa}$ $\newcommand{\weierp}[0]{\wp}$ $\newcommand{\Zeta}[0]{\mathrm{Z}}$

A Series Problem Based On Trigonometric Function.

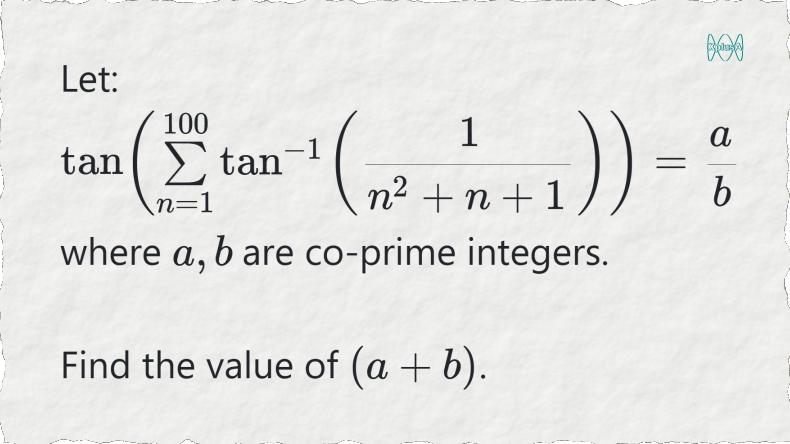
image containing math problem statement

A series problem based on trigonometric function. Can you spot the solution here? Try looking at it through a telescope.

Problem contributed by anonymous user

We can evaluate the LHS of the equation as follows:

$\tan \left( \sum \limits_{n=1}^{100} \tan^{-1}\left( \dfrac{1}{n^2 + n + 1} \right) \right)$

$= \tan \left( \sum \limits_{n=1}^{100} \tan^{-1}\left( \dfrac{1}{n(n + 1) + 1} \right) \right)$

-----------book page break-----------

$= \tan \left( \sum \limits_{n=1}^{100} \tan^{-1}\left( \dfrac{(n+1) - n}{1 + n(n + 1)} \right) \right)$

$= \tan \left( \sum \limits_{n=1}^{100} \left( \tan^{-1} (n+1) - \tan^{-1} (n) \right) \right)$

$= \tan \left( \left( \cancel{\tan^{-1}2} - \tan^{-1}1 \right) + \left( \cancel{\tan^{-1}3} - \cancel{\tan^{-1}2} \right) \right.$

$\left. + \left( \cancel{\tan^{-1}3} - \cancel{\tan^{-1}4} \right) + ... + \left( \tan^{-1}101 - \cancel{\tan^{-1}100} \right)\right)$

$= \tan \left( \tan^{-1}101 - \tan^{-1}1 \right)$

$= \tan \left( \tan^{-1} \left( \dfrac{101 - 1}{1 + 101 \cdot 1} \right) \right)$

$= \dfrac{50}{51}$

Therefore, $a = 50$, $b = 51$ and $(a + b) = 101$