A Relatively Simple Problem From The Polish Math Olympiad
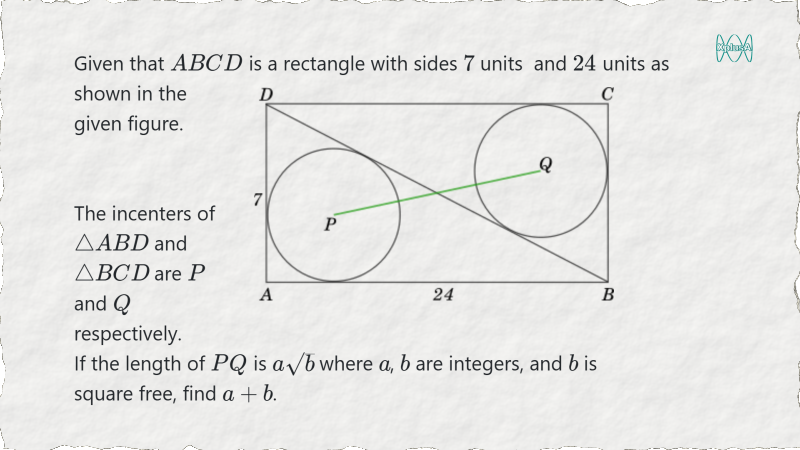
Here is a relatively simple plane geometry problem from the Polish Math Olympiad, which you can solve using a couple of very basic concepts.
-----------book page break-----------
Let us draw a line $RS$, parallel to $AD$ through point $P$ intersecting $AB$ and $CD$ at $R$ and $S$ respectively. We have drawn a perpendicular from $Q$ to $CD$ at $W$ as shown in the following figure:
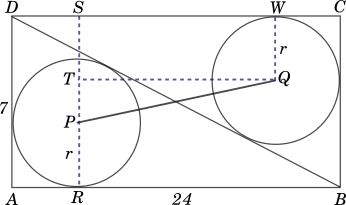
Since $ABCD$ is a rectangle and $BD$ is a diagonal,
$\triangle ABD \cong \triangle CDB$
Therefore the two incircles are also congruent, with equal radii.
Therefore, $PR = QW$. Let each be equal to $r$.
Since $\triangle ABD$ is right angled at $A$
$BD = \sqrt{AB^2 + AD^2} = \sqrt{24^2 + 7^2} = 25$
-----------book page break-----------
Using $\text{Corollary 4}$ of the theorem on , we can say that:
$area[\triangle ABD] = r \times s$ where $s$ is the semi-perimeter.
Therefore,
$area[\triangle ABD] = r \times \dfrac{7 + 24 + 25}{2} = r \times 28$
Also,
$area[\triangle ABD] = \dfrac{1}{2} \times AD \times AB= \dfrac{1}{2} \times 7 \times 24 = 84$
Therefore,
$r \times 28 = 84$
$\Rightarrow r = \dfrac{84}{28} = 3$
From the figure above, $ST = QW = r = 3$
Therefore, $TP = SR - PR - ST = 7 - 3 - 3 = 1$
Simlarly,
$QT = 24 - 3 - 3 = 18$
Therefore, using right angled $\triangle PTQ$ we get:
$PQ = \sqrt{PT^2 + TQ^2} = \sqrt{18^2 + 1^2} = \sqrt{325} = 5 \sqrt{13}$
Therefore,
$a = 5$ and $b = 13$, and $a + b = 18$