A Relatively Simple Problem From The 1962 Soviet Union Math Olympiad

-----------book page break-----------

Let us do the following additional construction, as shown in the figure below:

- Join diagonal $AC$.

- From point $C$ drop a perpendicular on $AB$ (extended, if needed) at $P$

- From point $C$ drop a perpendicular on $AB$ (extended, if needed) at $P'$

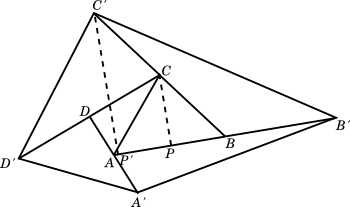
Considering $\triangle$s $CPB$ and $C'P'B$,

$C'P' \parallel CP$, therefore, $\triangle CPB \sim \triangle C'P'B$

Given that $CB = CC'$ therefore $BC' = 2 BC$

Due to similarity of triangles, $C'P' = 2CP$

-----------book page break-----------

Area of $\triangle CAB = \dfrac{1}{2} CP \times AB$

Area of $\triangle CBB' = \dfrac{1}{2} C'P' \times BB'$

$AB = BB'$ and $C'P' = 2CP$

Therefore, Area of $\triangle C'BB' = 2 \times $ Area of $\triangle CAB$

Similarly,

$Area[\triangle D'CC'] = 2 \times Area [\triangle DBC]$

$Area[\triangle A'DD'] = 2 \times Area [\triangle ACD]$

$Area[\triangle B'AA'] = 2 \times Area [\triangle BDA]$

$Area[A'B'C'D']$

$= Area[ABCD] + Area[\triangle C'BB'] + Area[\triangle D'CC']$

$+ Area[\triangle A'DD'] + Area[\triangle D'CC']$

$= Area[ABCD] + 2 \times Area [\triangle CAB] + 2 \times Area [\triangle DBC]$

$+ 2 \times Area [\triangle ACD] + 2 \times Area [\triangle BDA]$

$= Area[ABCD] + 4 \times Area[ABCD] = 5 \times Area[ABCD]$

Therefore,

$\dfrac{Area[A'B'C'D']}{Area[ABCD] }= 5$