Can You See What Is Not Apparent To The Eyes?
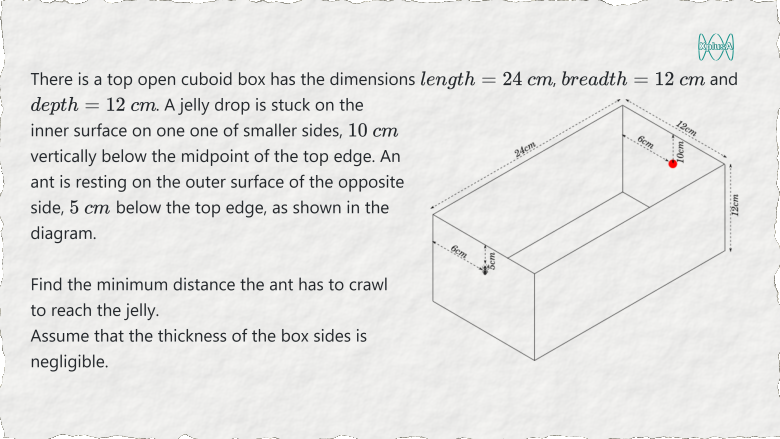
This problem may not have the answer that comes to the mind at a first glance. Take your time and try to think out of the box.
-----------book page break-----------
To be able to solve this problem we might have to examine a couple of possible paths.We know that the shortest distance between any two points is the straight line joining the two points on a plane.
In this case however, you cannot join the two points as the line will pass through space, and the ant cannot take that path.
So let us try to bring the two points on a single plane such that the ant can actually take that path.
Let us start by naming the vertices as shown in the figure below:
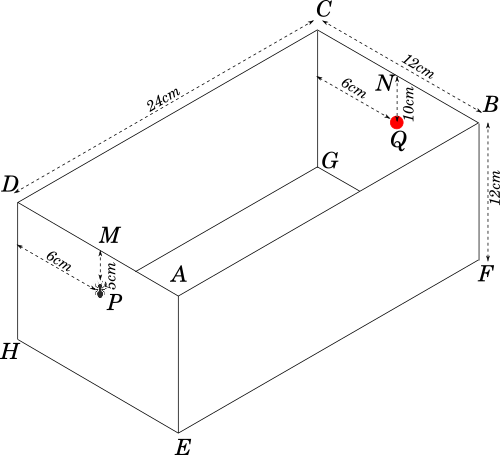
-----------book page break-----------
Now let us assume that the sides of the box are made of double layered material and can be unfolded along any edge of your choice. We can open the box as illustrated in the diagram below:

This way the two points $P$ and $Q$ are on the same plane and is a possible path for the ant.
And we get the length of the path as:
$5 + 12 + 24 + (12 - 10) = 43\ cm$
-----------book page break-----------
But there is one more possible path if we open the sides as shown in the following diagram:

To be able to find out the length of the paths in this case, let us consider $\triangle PMR$ and $\triangle QNR$
$\angle MRP = \angle NRQ$ $(vertically\ opposite\ angles)$ and $\angle PMR = \angle QNR$ (both $90^\circ$), therefore the thirds angles $\angle MPR$ and $\angle NQR$ are also equal.
$\therefore \triangle PMR \sim \triangle QNR$.
-----------book page break-----------
From the rules of similar triangles explained ,
$\dfrac{PR}{QR} = \dfrac{MR}{NR} = \dfrac{PM}{QN} = \dfrac{5}{10} = \dfrac{1}{2}$
$\therefore \dfrac{MR}{NR} = \dfrac{1}{2}$
$\Rightarrow NR = 2MR$
$MR + RN = MN = 6 + 24 + 6 = 36$
$\therefore MR + 2MR = 36$
$\Rightarrow 3MR = 36$
$\Rightarrow MR = 12$
$\therefore RN = 24$
Using Pythagoras theorem, we get:
$PR = \sqrt{PM^2 + MR^2} = \sqrt{5^2 + 12^2} = 13$
$\dfrac{PR}{QR} = \dfrac{PM}{QN} = \dfrac{1}{2}$
$\Rightarrow QR = 2PR = 26$
Total distance = $PR + QR = 13 + 26 = 39\ cm$
This path is less than the path we found in the previous approach, therefore this is the minimum path.
-----------book page break-----------
If we draw this path on the open surface and fold the sides back to the original position, the ant's path would look like:
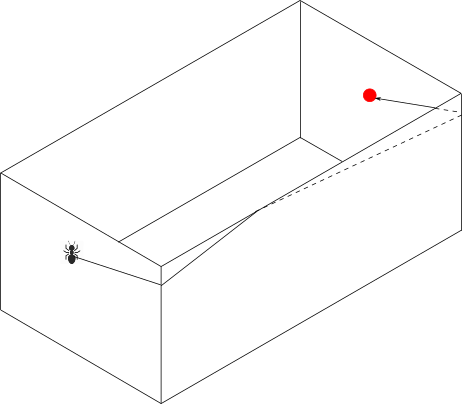
If you have difficulty visualising this path you can do the following steps:
- Fold an A4 size paper vertically through the middle.
-----------book page break-----------
- Fold it at two places, perpendicular to the first fold to form the $3$ sides through which the path goes.
- Mark a point on the outer surface for the ant and the opposite inner surface for the jelly.
- Unfold the paper and you will see that the ant and the jelly are on the same surface.
- Join these two points with a straight line.
- Fold the paper back. This should show you the path that the ant should take.