A Member Contributed Integration Problem Taken From The JEE Mains.
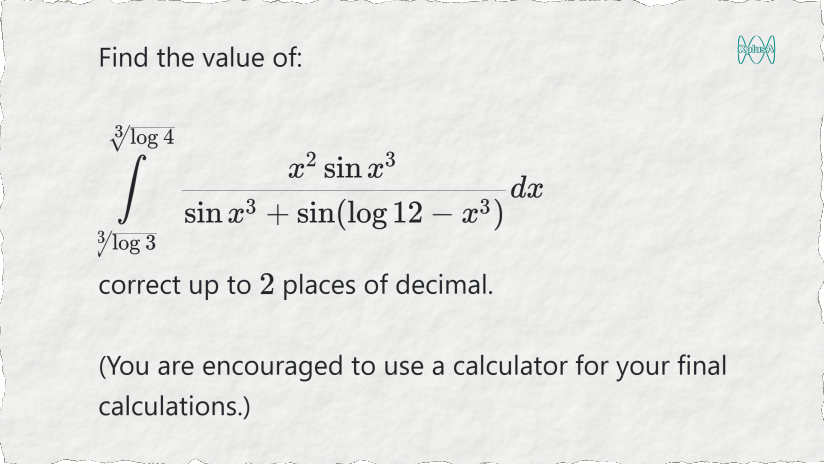
An adaptation of a relatively simple integration problem from JEE Mains as contributed by our community member. This problem is based on a neat and elegant trick.
Problem contributed by anonymous user
-----------book page break-----------
We will start using the substitution:$u = x^3$
Therefore, $du = 3x^2 dx$ and the limits $x=\sqrt[3]{\log 3} \longrightarrow u=\log 3$ and $x=\sqrt[3]{\log 4} \longrightarrow u=\log 4$
Therefore, we get the given integral as:
$\displaystyle \int \limits_{\log 3}^{\log 4} \dfrac{1}{3} \dfrac{\sin u}{\sin u + \sin (\log 12 - u)} du$
$= \displaystyle \dfrac{1}{3} \int \limits_{\log 3}^{\log 4} \dfrac{\sin u}{\sin u + \sin (\log 3 + \log 4 - u)} du$
We can see that the given integral is of the form:
$\displaystyle \int \limits_{a}^{b} \dfrac{f(x)}{f(x) + f(a + b - x)} dx$
Using the King's rule described , we can arrive at the answer:
$\displaystyle \int \limits_{\sqrt[3]{\log 3}}^{\sqrt[3]{\log 4}} \dfrac{x^2 \sin x^3}{\sin x^3 + \sin (\log 12 - x^3)} dx$
-----------book page break-----------
$= \dfrac{1}{3} \displaystyle \int \limits_{\log 3}^{\log 4} \dfrac{\sin u}{\sin u + \sin (\log 3 + \log 4 - u)} du$
$= \dfrac{1}{3} \dfrac{\log 4 - \log 3}{2}$
$= \dfrac{1}{6} \log \left(\dfrac{4}{3} \right)$
$\approx 0.02$