A Problem From The Stanford Math Tournament
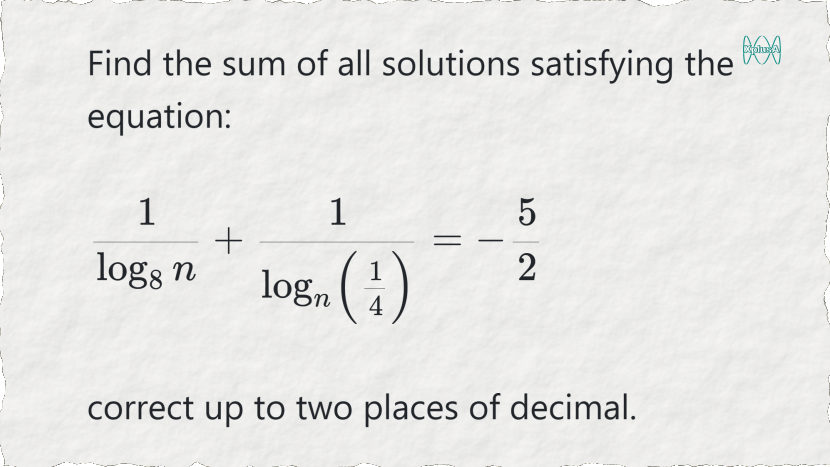
A problem selected from the Stanford Math Tournament. This problem was added by our member contributor.
Problem contributed by anonymous user
TBD
$\dfrac{1}{\log_8 n} + \dfrac{1}{\log_n \left( \frac{1}{4} \right) } = - \dfrac{5}{2}$
$\Rightarrow \log_n 8 + \dfrac{1}{\log_n \left( 2^{-2} \right) } = - \dfrac{5}{2}$
$\Rightarrow 3 \log_n 2 - \dfrac{1}{2\log_n \left( 2 \right) } = - \dfrac{5}{2}$
-----------book page break-----------
$\Rightarrow 6 (\log_n 2)^2 - 1 = -5 \log_n 2$
Substituting $x = \log_n 2$ we get:
$6 (x)^2 - 1 = -5 x$
$\Rightarrow 6x^2 + 5x - 1 = 0$
$\Rightarrow 6x^2 + 6x - x - 1 = 0$
$\Rightarrow (6x - 1)(x + 1) = 0$
$\Rightarrow \log_n 2 = \dfrac{1}{6}$ or $\log_n 2 = -1$
If $\log_n 2 = \dfrac{1}{6}$
$\Rightarrow \log_2 n = 6$
$\Rightarrow n = 2^6 = 64$
If $\log_n 2 = -1$
$\Rightarrow \log_2 n = -1 \Rightarrow n = 2^{-1} = \dfrac{1}{2}$
Therefore, sum of all solutions $= 64 + \dfrac{1}{2} = 64.5$