A Problem Based On One Of The Most Important Concept In Mathematics
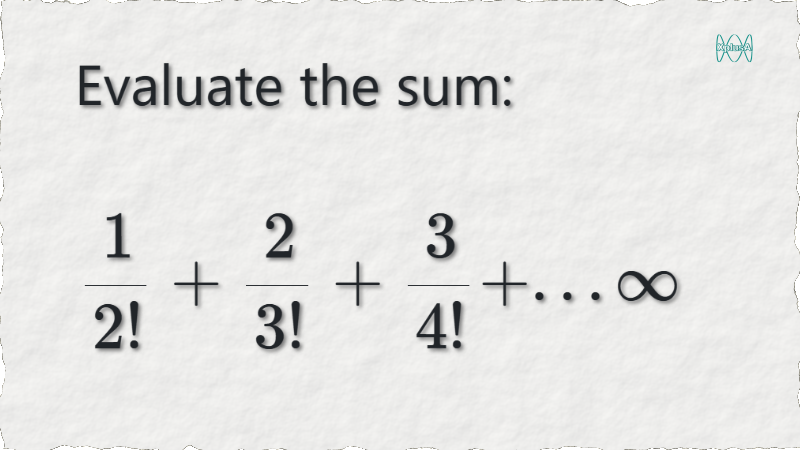
Do the terms of this series look familiar to you? This problem can expose you to a very important technique to solve series like this.
We will begin solving this problem starting with the definition of $e^x$, as given :
$e^x = \dfrac{x^0}{0!} + \dfrac{x^1}{1!} + \dfrac{x^2}{2!} + ... \infty$
$\Rightarrow e^x = 1 + \dfrac{x^1}{1!} + \dfrac{x^2}{2!} + ... \infty$
$\Rightarrow e^x = 1 + x \left(\dfrac{x^0}{1!} + \dfrac{x^1}{2!} + \dfrac{x^2}{3!} + ... \infty \right)$
-----------book page break-----------
$\Rightarrow e^x = 1 + x \left(\dfrac{x^0}{1!} + \dfrac{x^1}{2!} + \dfrac{x^2}{3!} + ... \infty \right)$
Differentiating both sides w.r.t. $x$:
$\dfrac{d}{dx}(e^x) = 0 + \dfrac{d}{dx} \left[x \left(\dfrac{x^0}{1!} + \dfrac{x^1}{2!} + \dfrac{x^2}{3!} + ... \infty \right)\right]$
$\Rightarrow e^x = \left(\dfrac{x^0}{1!} + \dfrac{x^1}{2!} + \dfrac{x^2}{3!} + ... \infty \right) + x\left(0 + \dfrac{x^0}{2!} + \dfrac{2x^1}{3!} +... \infty \right)$
$\Rightarrow e^x = \dfrac{1}{x}\left(\dfrac{x^1}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + ... \infty \right) + x\left(0 + \dfrac{x^0}{2!} + \dfrac{2x^1}{3!} +... \infty \right)$
$\Rightarrow e^x = \dfrac{1}{x} \left(1 + \dfrac{x^1}{1!} + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + ... \infty - 1\right) + x\left(\dfrac{x^0}{2!} + \dfrac{2x^1}{3!} + \dfrac{3x^2}{3!} +... \infty \right)$
$\Rightarrow e^x = \dfrac{1}{x} \left(e^x - 1\right) + x\left(\dfrac{x^0}{2!} + \dfrac{2x^1}{3!} + \dfrac{3x^2}{4!} +... \infty \right)$
Now substituting $x = 1$, we get:
$e^1 = \dfrac{1}{1} \left(e^1 - 1\right) + 1\left(\dfrac{1^0}{2!} + \dfrac{2 \cdot 1^1}{3!} + \dfrac{3 \cdot 1^2}{4!} +... \infty \right)$
$\Rightarrow \cancel{e^1} = \cancel{e^1} - 1 + \left(\dfrac{1}{2!} + \dfrac{2}{3!} + \dfrac{3}{4!} +... \infty \right)$
$\therefore \dfrac{1}{2!} + \dfrac{2}{3!} + \dfrac{3}{4!} +... \infty = 1$